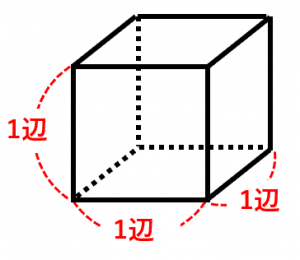
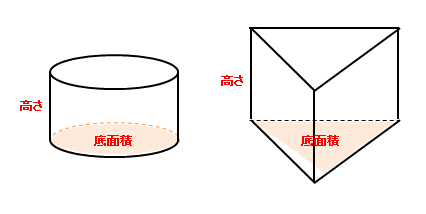
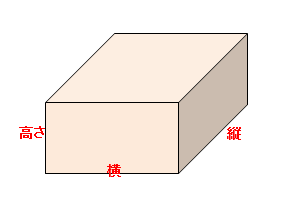
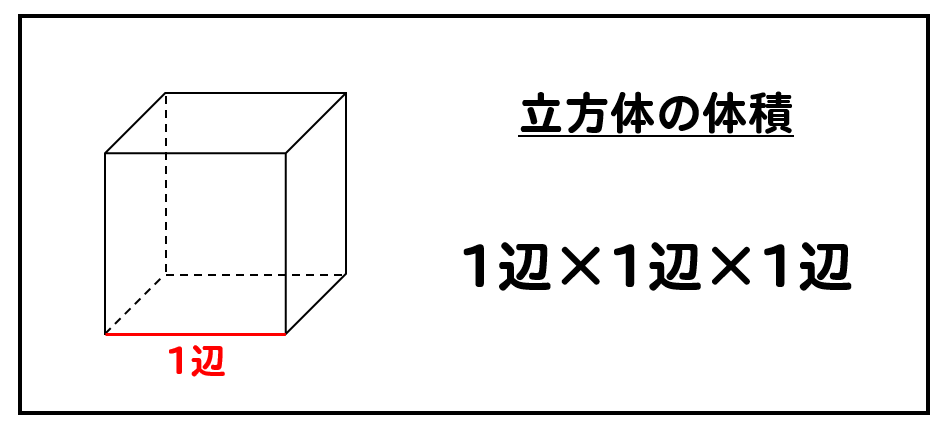
立体の体積を求める公式の一覧表 以上の立体の体積を求める公式を一覧表にまとめると、次の表のようになります。 立体 体積を求める公式 立方体 V = a3 V = a 3 直方体 V = abh V = a b h 三角柱 体積が求められるようになると1番最初に扱う立体が、立方体や直方体です。 立方体の体積を求める公式は、「一辺×一辺×一辺」。 直方体の体積を求める公式は、「たて×横×高さ」です。 覚えてしまえば、簡単に体積が求められますが立方体の公式を思い出してください。縦×横×高さでした。よって 立方体の体積=縦×横×高さ=3×4×5=60m 3 です。下図の問題も解きましょう。 上図は縦と横の長さが未知ですが、底面積の値が既知です。よって 立方体の公式=底面積×高さ=15×3=45m 3

小5 算数 小5 3 直方体と立方体の体積 Youtube
立方体 の 体積 を 求める 公式
立方体 の 体積 を 求める 公式-送信を完了しました。 立方体の体積 のアンケート記入欄 年齢 歳未満 歳代 30歳代 40歳代 50歳代 60歳以上 職業 小・中学生 高校・専門・大学生・大学院生 主婦 会社員・公務員 自営業 エンジニア 教師・研究員 その他 この計算式は 非常に役に 体積の求め方がわかりません 教えてください ①立方体の中に内接する球体があり立方体と球体の隙間にできる空間の容積は立方体の体積を1としたとき、いくつになるか。円周率πを用いて示せ。 ②底面積と高さが等しい円柱と円錐があります。
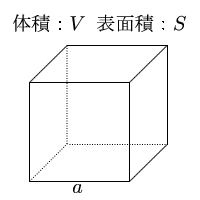



立方体の表面積から1辺 体積 表面積の計算 計算サイト
体積を求める立方体の辺の長さを入力して「計算」ボタンを押してください。 体積を入力して「計算」ボタンを押すと立方体の辺の長さが計算されます。 辺の長さと体積で異なる単位の計算も可能です。 例:辺の長さ500cm=体積125m 35年算数 体積の教え方1 子どもの学習支援by いっちに算数 体積の勉強は、体積の単位 や を理解させるとわかりやすくなります。 そのために2年「かさ」や4年「直方体と立方体」の勉強を元にして考えさせたいと思います。 忘れているお子さんには、上のリンク先でおさらいさせましょう。体積の公式 立方体は、角柱の一種といえます。 一辺×一辺×一辺は、底面積×高さと同じです。 直方体も角柱の一種といえます。 縦×横は、底面積といえるため、縦×横×高さも、底面積×高さと同じです。 角錐と円錐は、同じ式で体積を求めることでき
正三角形の面積について復習したい方はこちらも参照してください。 3分で分かる! 正三角形の面積の求め方・公式をわかりやすく もう一つ正四面体の体積の求め方を示しておきたいと思います。 それは正四面体に外接する立方体に着目し立方体の公式を下記に示します。 立方体の体積=a 3 aは1辺の長さです。その他の立体図形の体積の算定は下記が参考になります。 体積の公式は?1分でわかる求め方と覚え方、一覧、三角柱、円柱、三角錐の体積 実際に、下図の立方体の体積を求め ・直方体、立方体の体積を計算で求める方法を考える。 ・直方体、立方体の体積を求める公式をまとめる。 ・前時から計算で求める方法を考える。 ・1cm³の立方体の個数=たて、横、高さに気づき、公式にまとめる。 4 ・複合図形の体積の求め方を考え
まとめ! お疲れ様でした! 直方体や立方体の対角線の長さは、 2つの直角三角形に注目することで求めることができます。 ですが、公式を覚えておけば 計算の手間をかなり省けるのでおススメです! なので、公式をしっかりと使いこなせるようにしてたて,横,高さの辺の長さに気を付けて公式を使 えば,立体の体積を計算でかんたんに求めることが できる。 5 適用問題を解く。 6 本時の振り返り,自己評価をする。 直方体の体積=たて×横×高さ 立方体の体積=1辺×1辺×1辺 ・ 前時の学習を手がかりに 立体の体積の求め方(公式)を一覧にまとめました。 公式を忘れてしまったときには、こちらで確認しましょう。 体積の求め方公式 立方体・直方体の体積の求め方 円柱の体積の求め方 三角柱の体積の求め方 円錐の体積の求め方 四角錐の体積の求め方 注意 スポンサードリンク (adsbygoogle




立方体や直方体の体積の求め方を習ったら 少し応用的な問題にも取り組みましょう 展開図を見て 体積を求める問題や いくつかの立方体や直方体の面積を足したり引いたりして解く問題です 学習ノート 学習 小学校 算数




立方体の表面積と体積を求める公式と計算問題 単位との関係も ウルトラフリーダム
中学数学 中学2年生で学習する数学単元6つのまとめ 中3数学 3分でわかる!相似比から体積の比・表面積比を求める公式 直方体の体積は「縦×横×高さ」じゃなくても求められる どうも、わりと四角四面な一面も持っているジョンです 直方体の体積を求める『縦×横×高さ』 これは小学校で教わる算数の知識で、三つの辺の長さから体積を求める公式です。 例えば、次のよう2 右の立方体を、2点F,Hと、辺BC上の点P、辺CDの点Qを通る 平面で2つに分ける。(CP=CQ=4cm) このとき、点Gをふくむ側の立体の体積を答えなさい。 ≪ x を求める≫
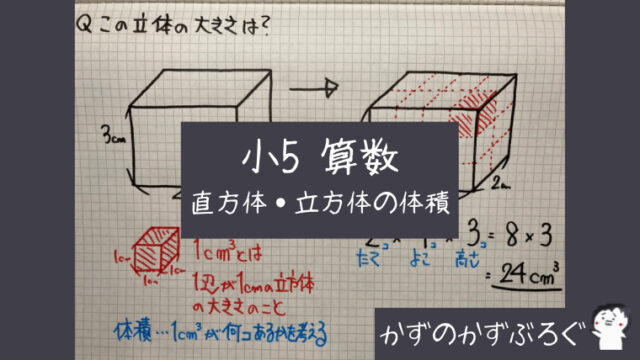



小5算数 直方体 立方体の体積 の問題 どこよりも簡単な解き方 求め方 かずのかずブログ




立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun
立方体 直方体 体積計算 公式 求め方 縦 横 自動 volume立方体の体積を求める計算式を覚える 立方体ではあらゆる辺の長さが等しいので、計算式もかなり簡単です。「1辺の長さ 3 」となります。 「1辺の長さ 3 」とは、その値を3回かけ算する、つまり、s 3 であれば、s × s × s、という意味です。それぞれの面積はこのように計算できます。 立方体の体積: 4× 4×4=64(cm3) 4 × 4 × 4 = 64 ( c m 3) 直方体の体積: 3× 4×5=60(cm3) 3 × 4 × 5 = 60 ( c m 3) つづいて、立方体・直方体がこれらの公式で求められる理由について説明していきます。




地図の体積計測




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強
また、一辺の長さが $10\\mathrm{cm}$ の立方体には水がちょうど1リットル入るということも分かります。 円柱の体積と水の容量 円柱の場合は円周率が現れるので、きれいな数字にはなりませんが、同じく 体積(立方センチメートル)を $1000$ で割ればリットル直方体や立方体の体積 直方体や立方体など、立体の体積の計算方法を学ぶよ。 動画で学ぼう! (NHK for School) (外部サイト) NHK 0959右の図のように,1辺の長さが 4 cmの立方体があり,辺 ab の中点を m ,辺 bc の中点を n とする。この立方体を4点 m, e, g, n を通る平面で2つの立体に切る。 このとき,次の(1)~(5)の各問いに答えなさい。 (4) 2つの立体のうち,頂点 b を含む立体の体積を求めよ。




6年算数角柱と円柱の体積 立体の体積 教え方




円柱の表面積と体積を求める公式 具体例で学ぶ数学
体積を求めよう ⑴直方体の体積は公式通りで求めることができますね ⑵立方体は、たて、横、高さが同じになるので 立方体の体積=1辺×1辺×1辺 と別の公式で表すことができます ⑶展開図で図形が書いてある場合は それを組み立てた図を書いて たて立方体の体積の公式は次のとおり。 立方体の体積の公式 ・ 立方体の体積\ (\hskip2pt=\hskip2pt\)\ (1\)辺\ (\hskip2pt\times\hskip2pt\)\ (1\)辺\ (\hskip2pt\times\hskip2pt\)\ (1\)辺 立方体の体積の求め方を見ていきましょう。 立方体の体積を求める問題 まずは問題です。 問題直方体の体積を求める公式を導 き出す。(スマートボードで直方 体を示し、1㎤の数を数える) 「公式を使った答えの求め方」を 練習問題で学習する。 練習問題2問を自力で解く。 立方体の体積を求める公式を導 き出す。(スマートボードで立方



質量の求め方は 1分でわかる公式と求め方 体積 密度との関係 求め方




立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun
大きな体積の単位 (立法メートル)を使って、直方体の体積を求めると次のようになります。 直方体の体積は、たて×横×高さで求められるので、 式 (24りっぽうめーとる と読みます) 教え方4-② 1 の立方体の体積を使って、 と の関係を教えます。 問題 球の体積の求め方の公式が覚えられねえ!! こんにちは!この記事をかいているKenだよ。ビニール傘を買っちゃったね。 球の体積の求め方には公式があるんだ。 球の半径をrとすると、体積の求め方は、 $$\frac{4}{3}πr^3$$ になるよ。 つまり、よって、立方体から余った体積を引けば、正四面体の体積を導き出すことができます。 正四面体の1辺の長さを a とします。 余った部分は全部で4つありますが、辺の長さは全てそれぞれ等しいので、これらは合同になります。




マスラボ 小学校5年 体積 レベル3 立方体の体積の求め方 Youtube
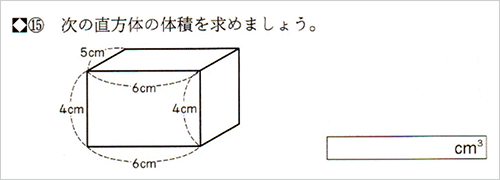



私の実践 私の工夫 算数 直方体や立方体の体積 児童が既習の知識と結び付けて考察できる授業を目指して 啓林館
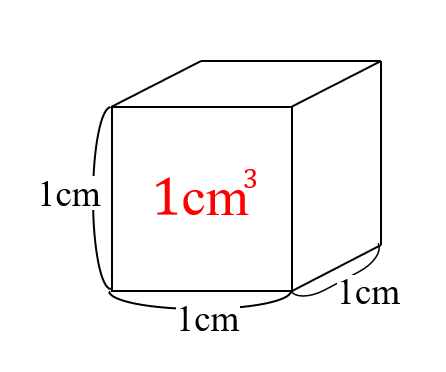
立体の体積 角柱、円柱の体積 柱の体積 = 底面積 × 高さ (例) 三角柱 高さ8cm 底面積 5cm 2 体積=5×8=40 四角柱(直方体) 4cm 3cm 8cm 底面積=4×3=12 体積=12×8=96 半径5cm 高さ 8cm 円柱 底面積=5×5×π=25π 体積=25π×8=0π 例題次の立体の体積を求めよ。 底面積15cm 2, 高さ6cmの五角柱 底面の半径2cm, 高さ10cm 立方体 / 直方体 の体積を求める公式 立方体と直方体の体積を求める公式は、縦 ( たて ) × 横 ( よこ ) × 高さ ( たかさ ) です。 簡単ですね。 例えば、縦、横、高さがすべて 3cm の立方体の体積は 3 cm × 3 cm × 3 cm = 9 cm 3 となります。 体積の 単位に注目してみましょう 。
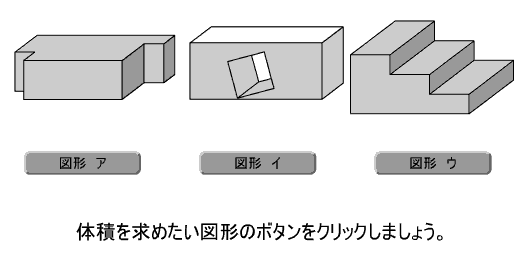



算数科5年 体積 導入 発展教材ソフトを使った授業 Note Board




面積や体積のかけ算の順序 おかしな算数教育 身勝手な主張
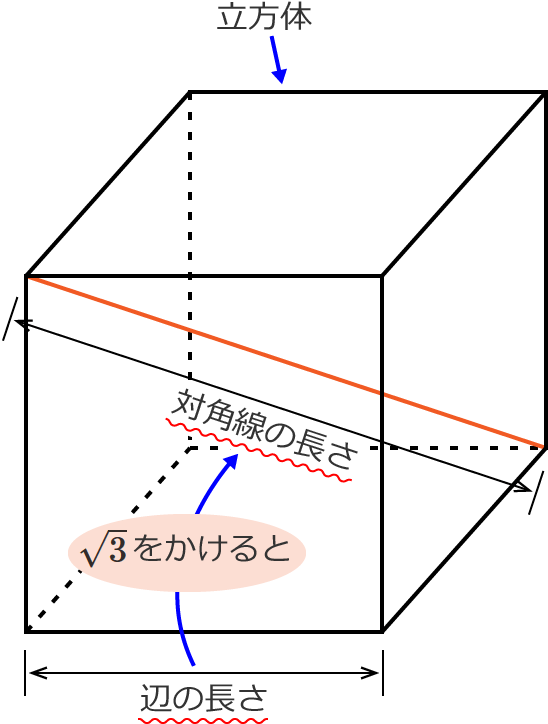



立方体の対角線の長さの求め方




計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学




どうして1 3なの 錐の体積の公式の求め方 まなべーと




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強




複雑な形の立体の体積 小学生の算数質問ひろば 進研ゼミ小学講座




立方体の表面積と体積を求める公式と計算問題 単位との関係も ウルトラフリーダム




中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット




立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun
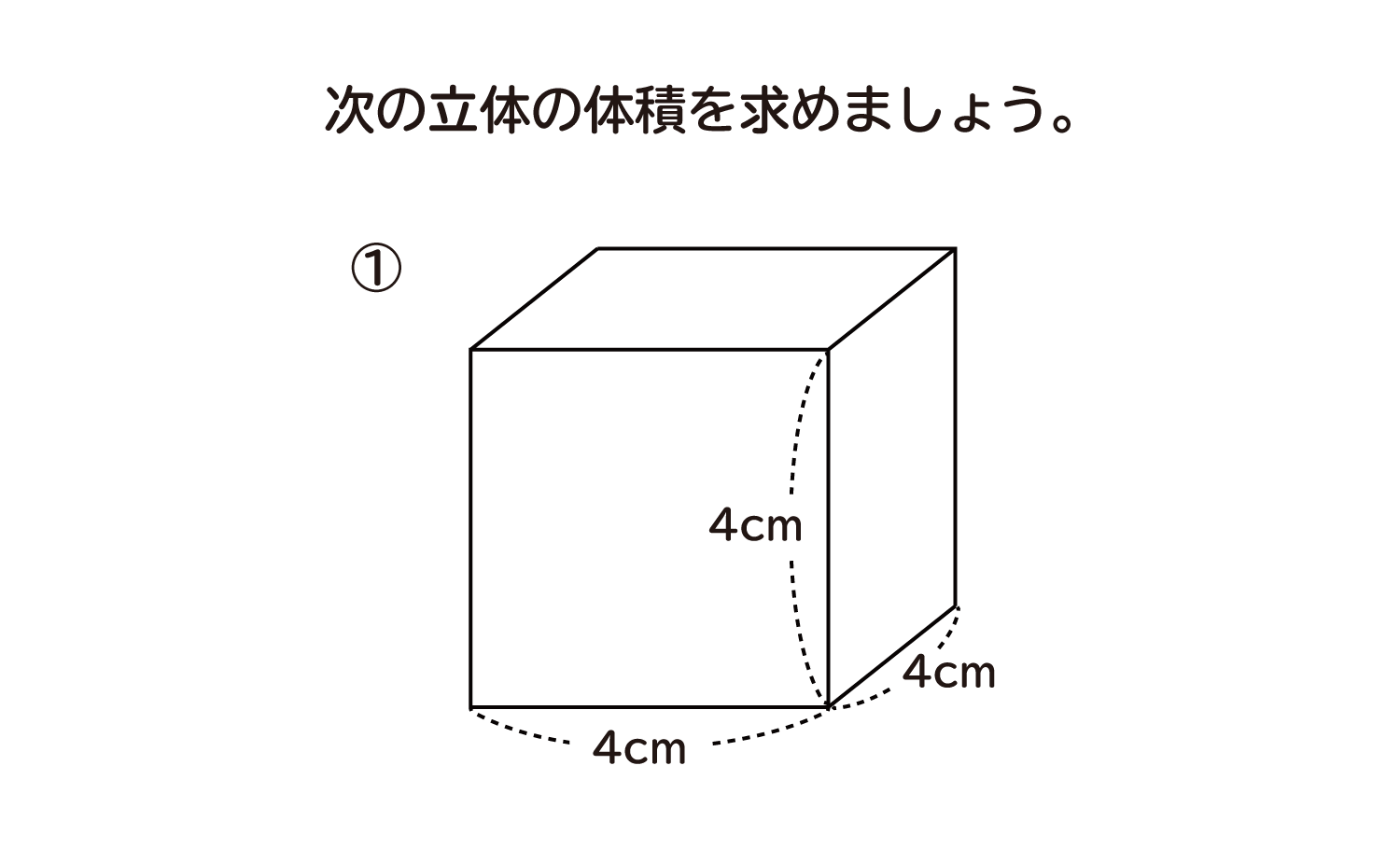



小学5年生 算数 無料問題集 直方体や立方体の体積 おかわりドリル



6年算数角柱と円柱の体積 立体の体積 教え方



立方体の公式は 1分でわかる意味 体積の公式と例題の求め方 表面積の公式




私の実践 私の工夫 算数 直方体や立方体の体積 児童が既習の知識と結び付けて考察できる授業を目指して 啓林館




小5 算数 小5 3 直方体と立方体の体積 Youtube



5年算数体積 容積の求め方 わかる教え方



立方体の表面積の求め方は 1分でわかる計算 公式 直方体の表面積の求め方



5年算数体積 容積の求め方 わかる教え方




中学受験 算数 立体図形の体積の求め方 公式の成り立ちから詳しく解説 中学受験アンサー
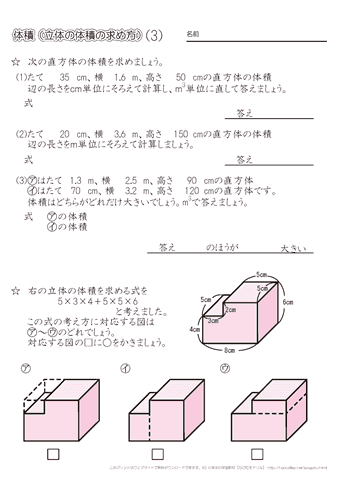



小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生
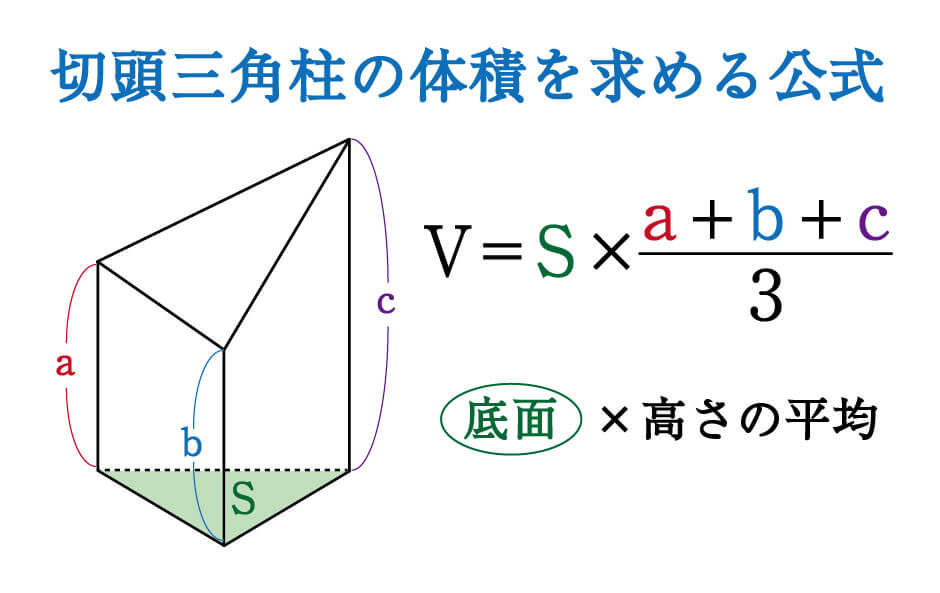



数学 斜めに切断された三角柱の体積は こう解くべし 受験の秒殺テク 7 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



立方体と直方体の体積を計算する方法とツール 具体例で学ぶ数学



兵庫県実践事例 算数小学校6年




立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun



小学算数 立体の体積の公式と単位 立方体 直方体 円柱 三角柱 偏差値40プログラマー



立方体の公式は 1分でわかる意味 体積の公式と例題の求め方 表面積の公式




すきるまドリル 小学5年生 算数 体積 無料学習プリント すきるまドリル 幼児 小学生の無料学習プリント




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強




円柱の体積の求め方 公式 小学生 中学生の勉強




立方体の表面積を求める計算と公式 辺と表面積の対応表つき Irohabook



小学算数 立体の体積の公式と単位 立方体 直方体 円柱 三角柱 偏差値40プログラマー




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強



算数科予習プリント 体積の求め方は考えられたかな 翁島 おきなしま 小学校ホームページ




円柱の体積の求め方 公式 小学生 中学生の勉強
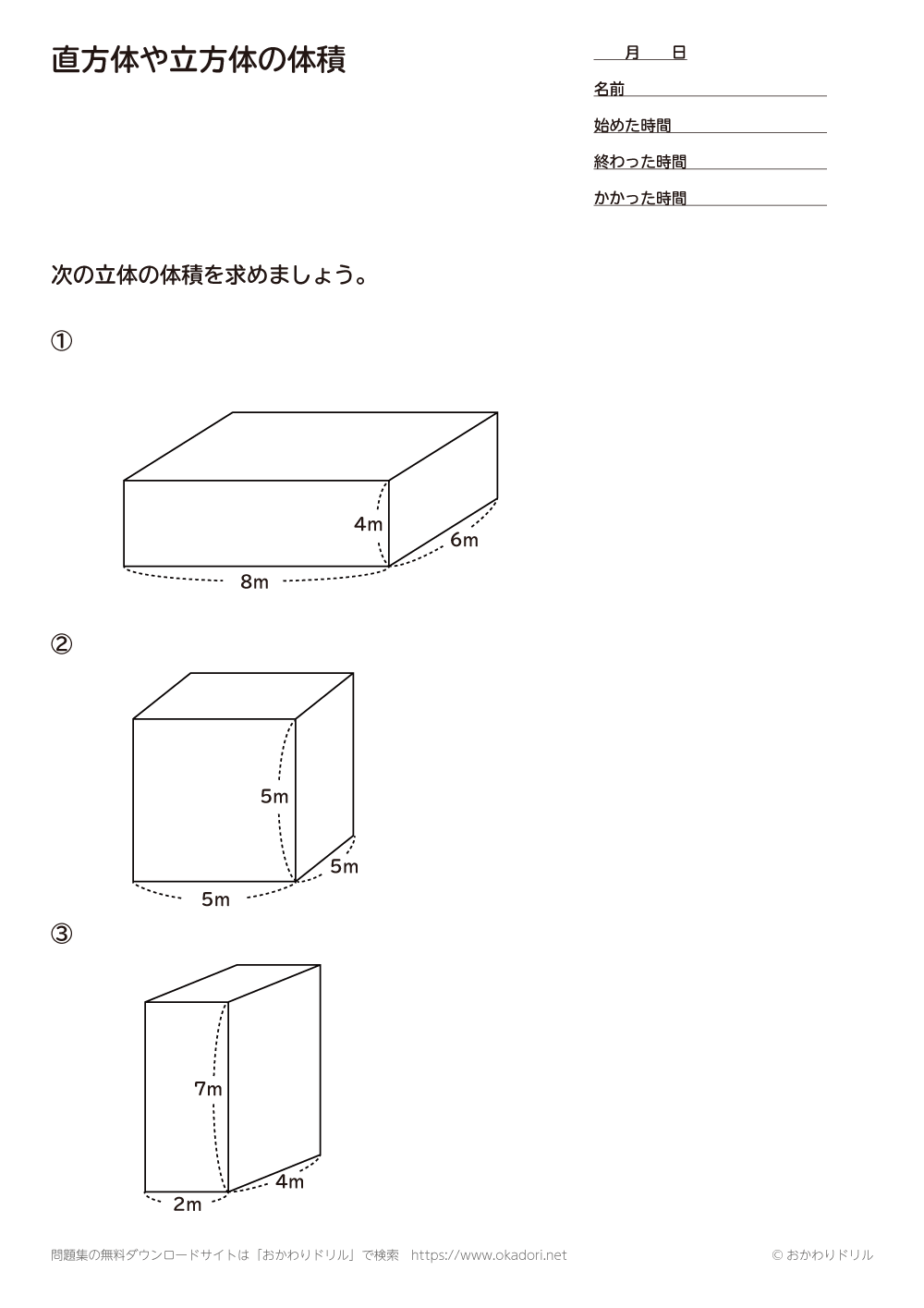



小学5年生 算数 無料問題集 直方体や立方体の体積 おかわりドリル



立方体の体積 小学生はどうやって問題解く 計算のやり方を解説 数スタ




小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生
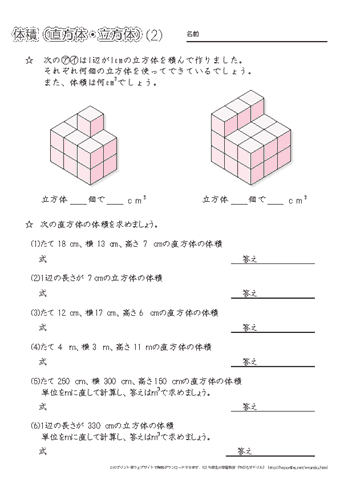



小学5年生の算数 体積 直方体と立方体の体積の求め方 練習プリント ちびむすドリル 小学生




容積の求め方 小学生の算数質問ひろば 進研ゼミ小学講座




計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




小5 算数 小5 5 体積の求め方のくふう Youtube




立方体の体積の求め方 滴水館道場




多くの教師が失敗する角柱の体積の求め方 算数を究める



5年算数体積 容積の求め方 わかる教え方



1
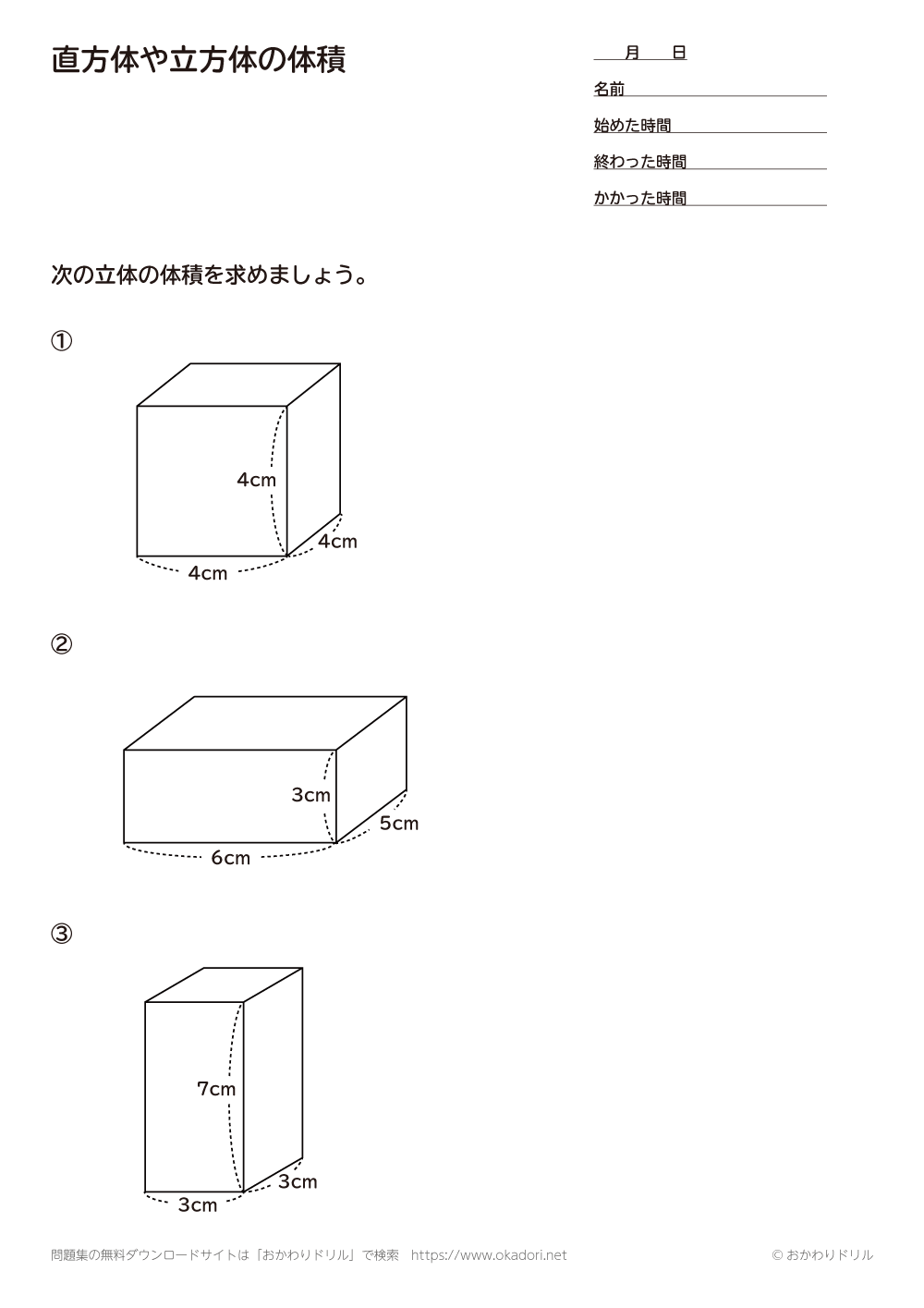



小学5年生 算数 無料問題集 直方体や立方体の体積 おかわりドリル




計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




面積や体積のかけ算の順序 おかしな算数教育 身勝手な主張




体積の求め方 計算公式一覧



立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun




โน ตของ 体積の求め方 立方体 長方体 ช น Primary算数 Clearnote




立方体の表面積から1辺 体積 表面積の計算 計算サイト



立方体の体積は 1分でわかる計算 単位 公式 求め方 リットルとの関係




体積の求め方 計算公式一覧




直方体と立方体の体積 算数 数学が好きになりmath




体積の求め方 計算公式一覧
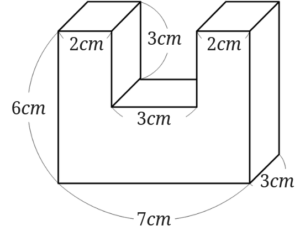



直方体や立方体の体積を求める応用問題の解き方は どうやって教えるといいの みけねこ小学校




小5 複雑な立体の体積 直方体 日本語版 Youtube



体積の応用




三角錐 四面体 の体積の公式 Schoolmath S Diary




角柱の体積の公式 求め方は底面積と高さに注目するだけだ 中学や高校の数学の計算問題




角柱 円柱の体積の公式 小学生に教えるための分かりやすい解説 数学fun



5年算数体積 容積の求め方 わかる教え方




計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく
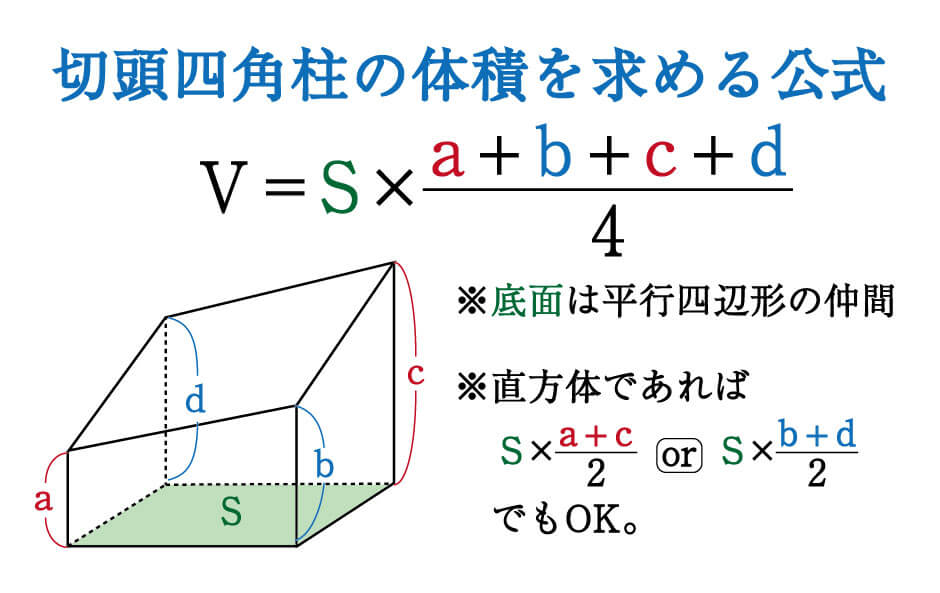



数学 斜めに切断された円柱 四角柱の体積は こう解くべし 受験の秒殺テク 6 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
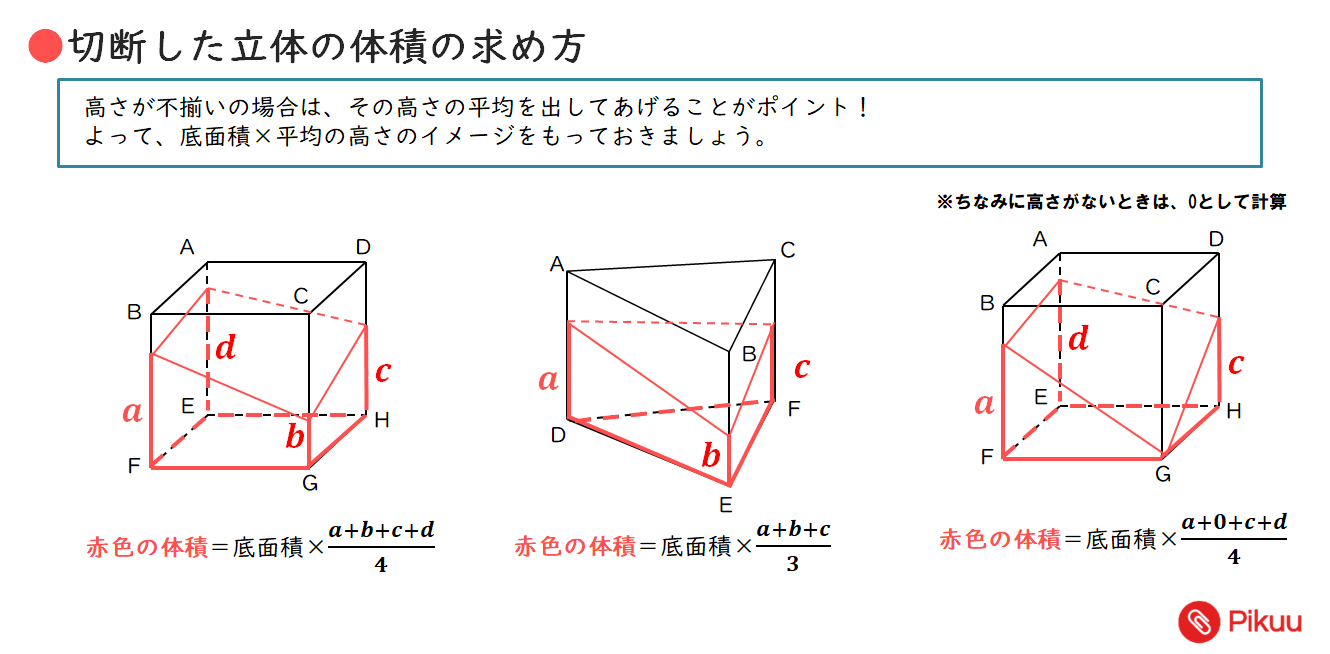



高校入試対策数学 切断した立体の体積を求める練習問題 Pikuu




四角錐台の体積 高精度計算サイト




公式を図解 すい体の体積 円すいの表面積 の公式の求め方と使い方 中学受験ナビ




体積の測定 測定のことを 即 知りたい ソクシリ キーエンス
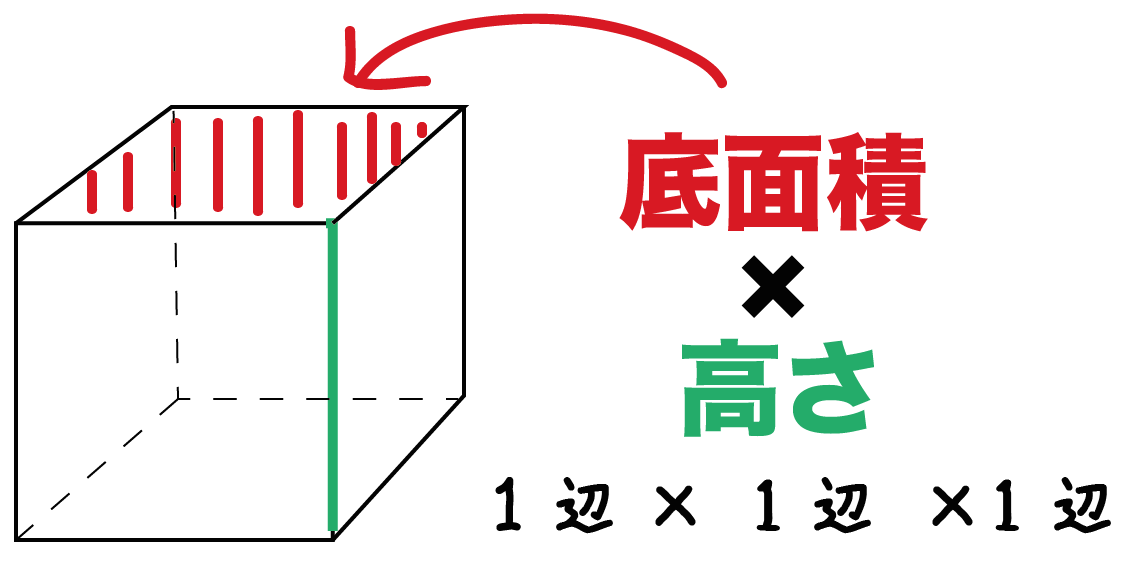



計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学
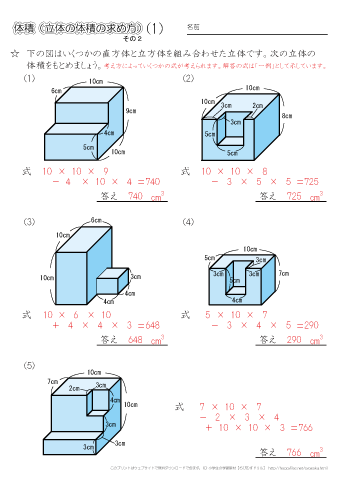



小学5年生の算数 体積 直方体と立方体を組み合わせた立体の体積を求める問題 ちびむすドリル 小学生




小学5年生の算数 動画 体積の求め方のくふうの問題 19ch



3




計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生




直方体や立方体の体積を求める公式は どうして たて 横 高さ なの みけねこ小学校




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード
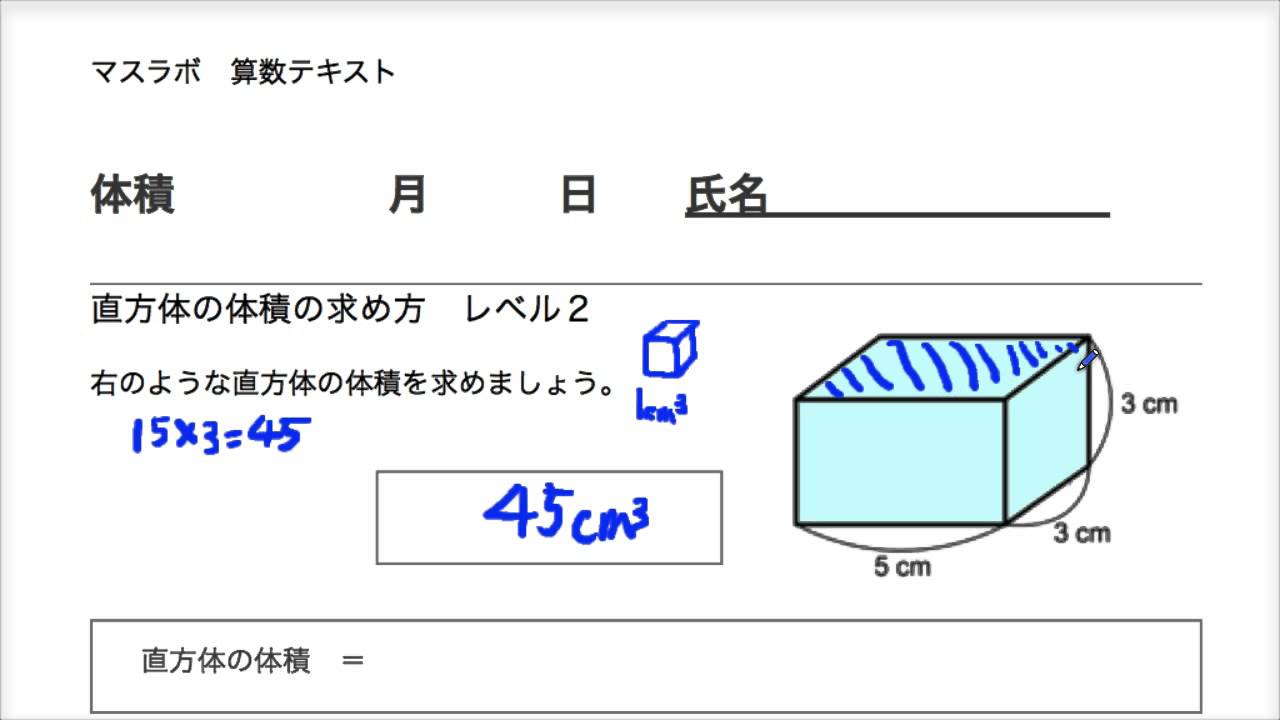



マスラボ 小学校5年 体積 レベル2 直方体の体積の求め方 Youtube
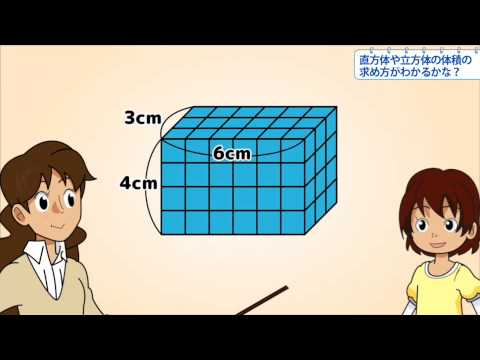



小5算数 直方体や立方体の体積の求め方がわかるかな Youtube



立方体 直方体の体積と公式 体積計算機




立体の体積を求める公式




体積の求め方 計算公式一覧



3




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




計算公式 立方体の表面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




5年 直方体と立方体の体積 算数イメージ動画集 大日本図書
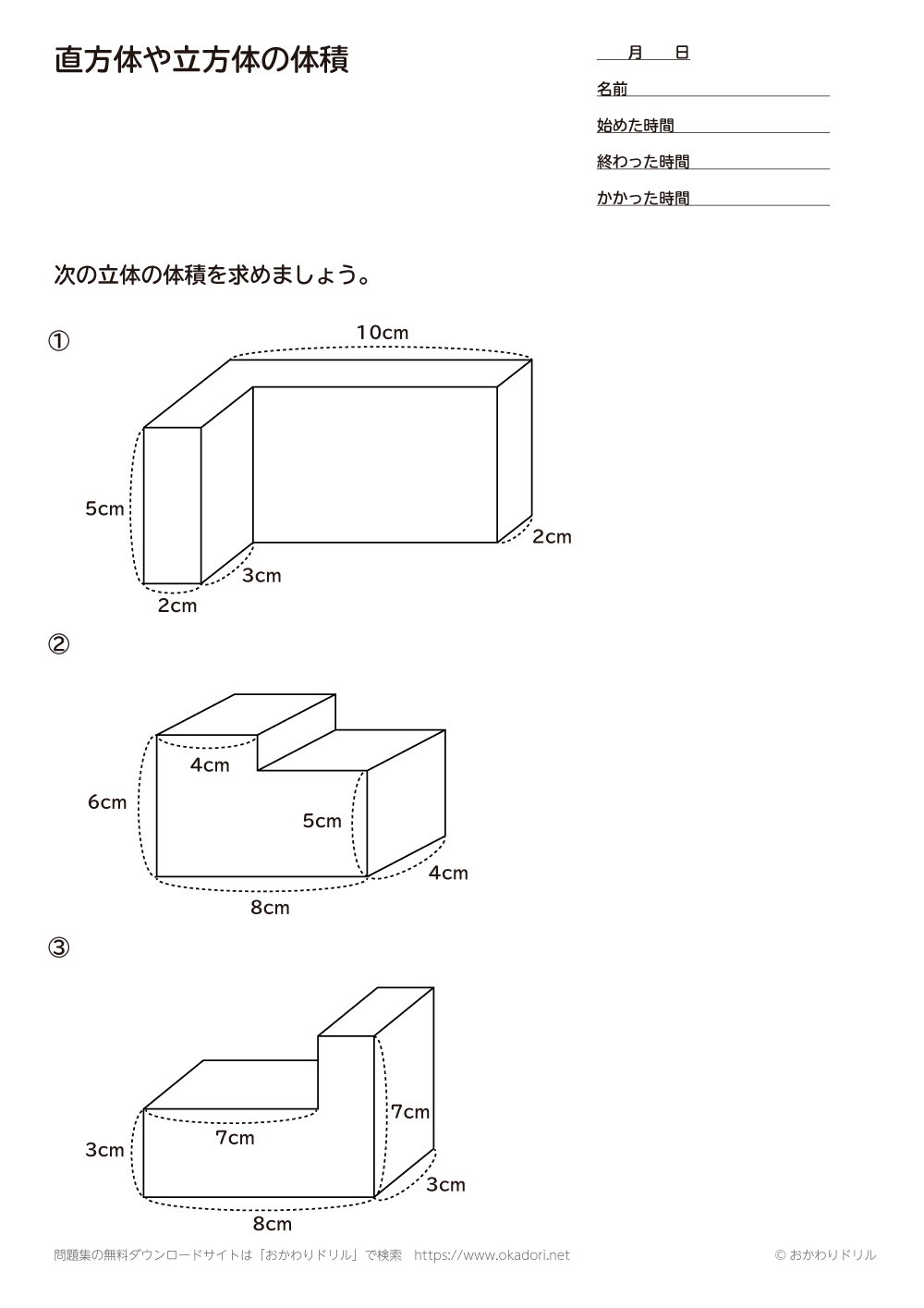



小学5年生 算数 無料問題集 直方体や立方体の体積 おかわりドリル



1



直方体の体積の公式は 1分でわかる求め方 例題 直方体の面積の公式



0 件のコメント:
コメントを投稿