++ 50 ++ ベクトル 3角形の面積 296966-ベクトル 3角形の面積

空間座標，空間ベクトル 公式と例題 このページは，空間座標や空間ベクトルの基本公式を広く浅く取り上げ，次に簡単な例題を示したものです． この部分は，教科書や授業では，平面座標・平面ベクトルと内容的に重なることが多く，空間座標・空間 正多角形をすべての対角線で分けた二等辺三角形の面積を求めて、その和を求める方法もあるので、上記の公式を無理して覚える必要はありません。 （二等辺三角形に分ける方法については、計算問題①で解説します！） 正 n 角形の面積の公式（n = 3, 4, 5, 6）10 第3章線形代数 (2) OABの面積をx1,y1,x2,y2 で表せ (3) OAC の面積をx1,y1,x2,y2,x3,y3 で表せ 3 4 平面π はベクトル −→ A = a −→ i b −→ j c −→ k と直交している 平面π から離れた点P(x,y,z)をとり, π 上に点 P0(x0,y0,z0)をとる また, ベクトル −→ A と直交するベクトル −−−→ P0P1 をつくる

勉強しよう数学 三角形の面積をベクトルで分解して計算する

ベクトル 3角形の面積

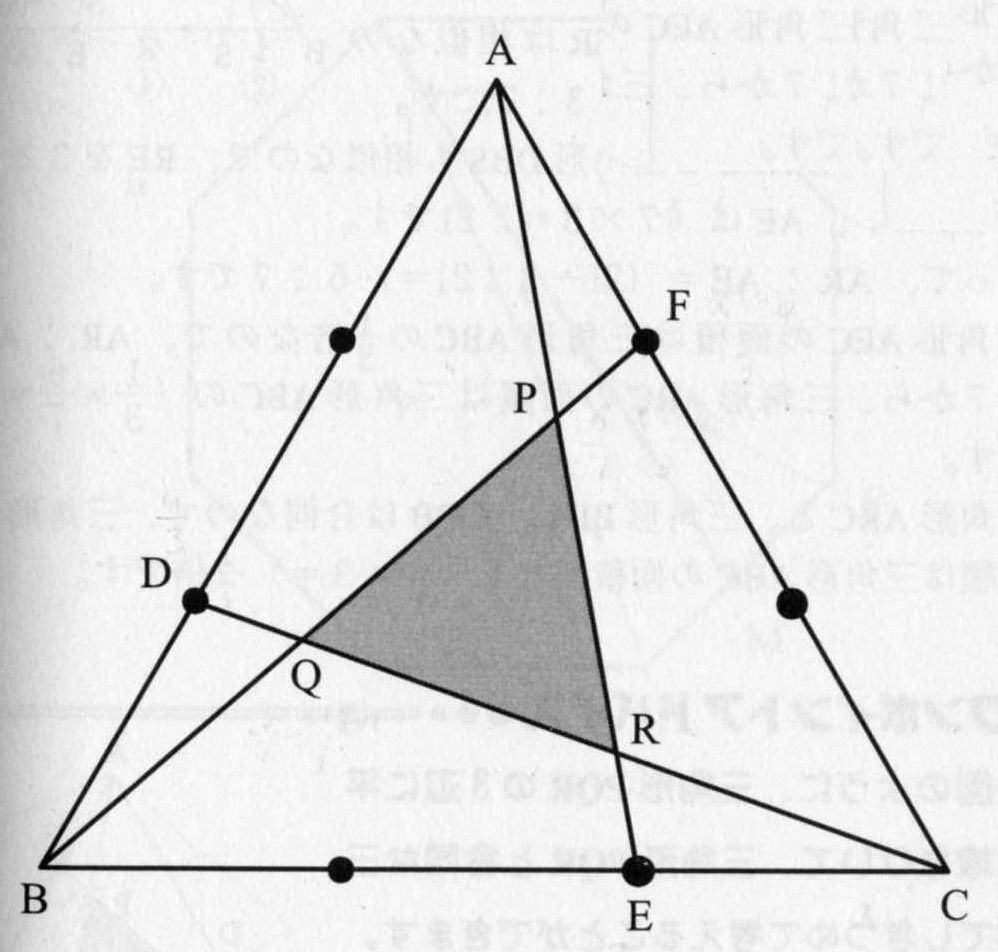
ベクトル 3角形の面積-また，3つの角がそれぞれ等しいので三角形 b a d bad b a d と三角形 b e c bec bec は相似であり， B A A C = B A A E = B D D C BAAC=BAAE=BDDC B A A C = B A A E = B D D C ベクトル 本記事では, ベクトルの分野で基本的な3つの面積公式とその導出方法を紹介します。 三角形の面積公式 → OA = →a(a1, a2) → OB = →b(b1, b2) とすると 三角形OABの面積 S は (1)S = 1 2 →a →b sinθ (2)S = 1 2√ →a 2 →b 2 − (→a ⋅ →b)2 (3

ベクトルの公式一覧 計算 内積 三角形の面積 共線条件 理系ラボ

複素数平面を使うと「3つの複素数の交代式の簡単化公式」、このクロス積を展開してもさほど複雑では無い対称式でクロス積の内容をあらわすことができます。 リンク： 三角形の面積をベクトルで分解して計算する 高校数学の目次1 ベクトルの基礎 6/14 B A A B B A u A B A Bsin 図16 ベクトルの外積 平行四辺形の面積 は図16に示す2つのベクトルのなす角度である．方向を表すuは単位ベクトルで，ベク トルAを Bの方に向かって回したときに，右ネジの進む方向と定義する．ベクトルの大き さは，右図のようにベクトルAと Bが作ベクトルを用いて3角形の面積を計算する 図2 ベクトル図 図2のように、点1から点2のベクトルA=(xa,ya)とし、 点1から点3のベクトルB=(xb,yb)とすると、 (xa,ya) = (x2,y2) (x1,y1) (xb,yb) = (x3,y3) (x1,y1) となる。 ベクトル(xa,ya)とベクトル(xb,yb)が作る平行四辺形の面積は C = xa・yb ya・xb となる。

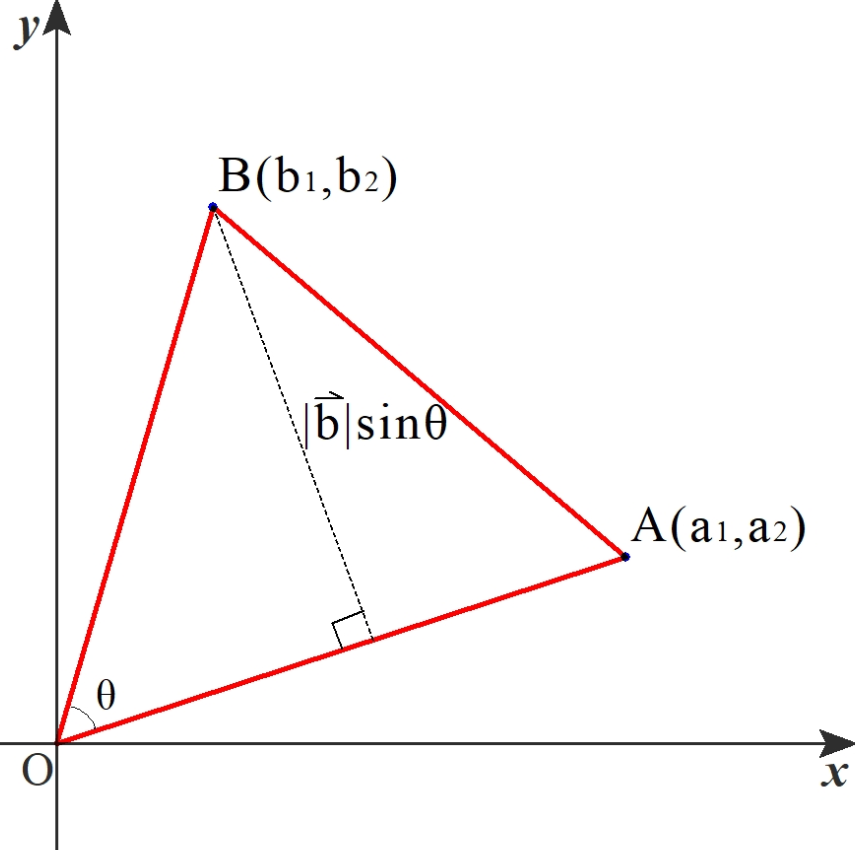
 ベクトルの成分と三角形の面積 先ほどの式を、成分で考えてみましょう。すると、これもきれいな式が得られます。 $\vec{a}=(a_1,a_2)$, $\vec{b}=(b_1,b_2)$ として、ルートの中を計算していきましょう。基本ベクトルの内積と成分で見た内容などを使って 外接円の半径の公式 公式①正弦定理から求める 公式②3 辺と面積から求める 外接円の半径の求め方例題 外接円の性質 性質①外心（外接円の中心）と垂直二等分線 性質②外心と各頂点との距離 外接円の書き方 外接円の練習問題 三角形の重心の位置ベクトル g g → とおいて、これについて考えましょう。 重心 G は、 AP を 2 1 2 1 に内分します。 再び、上で見た内分点の式から c 3 g → = a → 2 p → 2 1 = a → 2 × b → c → 2 3 = a → b → c → 3 となります。 3つの頂点の位置ベクトルを足して3で割ったものが重心の位置ベクトルになるんですね。 これも覚えやすいですね。 g g → につい

ベクトルの大きさを求めることと、線分の長さを求めることは同じことといっても良いですが、 ベクトルの内積を利用する際の求め方でやってはいけない注意点とともに基本的な問題で復習しておきましょう。 ベクトルな便利さ 三角比の余辺a、辺b、辺cを入力し「三角形の面積を計算」ボタンをクリックすると3辺の長さから三角形の面積を計算して表示します。 辺 a： 辺 b： 3点からなる三角形の面積を求める 外積 を用いて三角形の面積を求める方法を紹介します。 まず、 外積 のおさらいですが、三次元ベクトルにおいて2つのベクトルの外積の大きさが2つのベクトルからなる平行四辺形の大きさに一致する特徴がありました。 この2つのベクトルのZ成分を0（ゼロ）にして二次元座標へ応用します。 とすると、2つのベクトルの外積は、x

1

2つの線分の交点の位置ベクトルや内分比を求める裏技 教師用

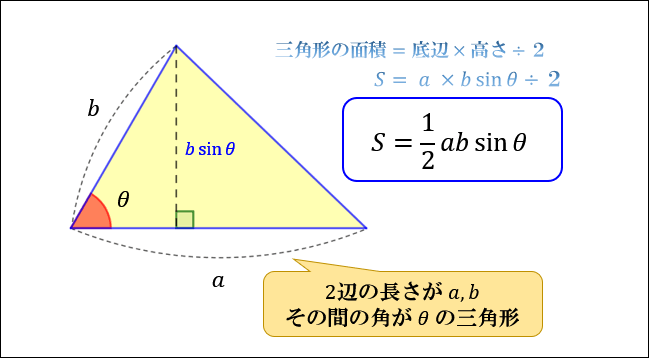
三角形の面積の求め方まとめ。 タイプ別でわかる公式一覧 Tooda Yuuto 18年9月26日 / 19年1月3日 三角形の面積は「 底 辺 × 高 さ ÷ 2 底 辺 高 さ 」という公式から求まりますが、この公式以外にも色々な方法で三角形の面積を求めることができます。 このページでは、そんな三角形の面積の求め方をタイプ別に見ていきましょう。 スポンサーリンク三角形の3辺が与えられたときの面積の求め方 「3辺の長さが，5，4，7の三角形の面積を求めよ。 」という問題がわかりません。 面積を求めるときは，公式 S＝1/2 bc sin A に当てはめればいいことは知っています。 しかし，この公式を使うには， A の大きさが必要ですが，問題で与えられていないので，この公式が使えません。 どうやって求めたらいいのですか13 Fubini の定理 7 図のように切ると底辺2x，高さpx 2 の三角形になるので，その面積は x2 p 2 ，したがって 2 ∫p 2 0 x p 2 dx= 4 3 13 Fubiniの定理

勉強しよう数学 三角形の３頂点のベクトルの張る三角形の面積比の公式

48s96ub7b0z5f Net Kuukan Bekutoru Menseki

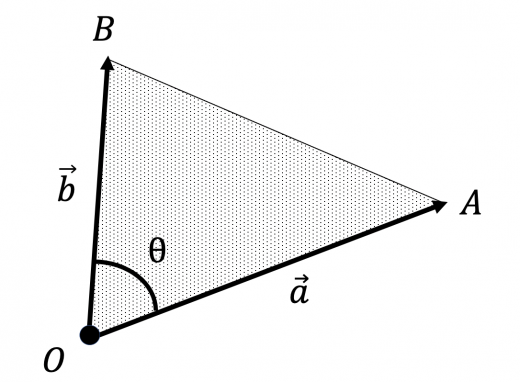
はじめに ここでは、ベクトルを用いた三角形の面積の求め方、その公式について説明しています。 面積を求める公式 図のように、 と で張られる三角形の面積をSとします。 このとき、面積Sは、次のように表すことができます。 これをベクトルを用いて3角形の面積を計算する 図2 ベクトル図 図2のように、点1から点2のベクトルA=(xa,ya,za)とし、 点1から点3のベクトルB=(xb,yb,zb)とすると、 (xa,ya,za) = (x2,y2,z2) (x1,y1,z1) (xb,yb,zb) = (x3,y3,z3) (x1,y1,z1) となる。 ベクトルA 、ベクトルB の外積(xg,yg,zg)は次式となる。 A×B ＝ （ya・zb－za・yb，za・xb－xa・zb，xa・yb－ya・xb）12 外積(ベクトル積) 空間ベクトル(3 次元ベクトル) a,b (‰ 0) が平行でないとき, a,b の両方と直交し, a,b,n が右手系(下で説明す る) となるような大きさ1 のベクトルn が一意に定まる このとき, a,b のなす角をθ (0 ő θ ő π) として, a とb の外積aˆb を

斜辺10cm 高さ6cmの ありえない 直角三角形の面積を真面目に求める

ベクトルを用いた三角形 平行四辺形の面積の公式と求め方 高校生向け受験応援メディア 受験のミカタ

 行列？ adbc 3次元 A (a,b,c),B (d,e,f) 内積 A・B＝ (a,b,c)・ (d,e,f)＝√（a^2b^2c^2）*√（d^2e^2f^2）*cosθ 外積 A×B＝ (a,b,c)× (d,e,f)＝√（a^2b^2c^2）*√（d^2e^2f^2）*sinθ 外積の絶対値 bfeccdfaaedbではなく、SQRT { (AA) (BB) (AB)^2} 行列？ bfeccdfaaedb3次元ではたまたま 3 c 2 ＝3 なのでベクトルとして表現できますし， 2次元ではたまたま 2 c 2 ＝1 なのでスカラーとして表現できます． 一般のN次元では，ベクトル a＝(a 1, a 2, , a n) と b＝(b 1, b 2, , b n) の外積は，次のような n×n 行列で表現できます．(3)，(4)，(5)を(1)に代入すると(2)が求まる． ホーム>>カテゴリー分類>>ベクトル>>三角形の面積 最終更新日： 15年10月5日 ページ

勉強しよう数学 三角形の面積をベクトルで分解して計算する

ベクトルによる三角形の面積の求め方 公式や証明 計算問題 受験辞典

3次元空間内の面積 3次元の中にある面積はベクトルで表現される と言うとビックリされることが多い。 面積ベクトルは、大きさ（ベクトルの長さ）として面積の絶対値を持ち、向きはその法線方向 面積に対し垂直なベクトルを「法線ベクトル」と呼ぶCreated Date 12/1/10 236 PM 2ab\,の成分は,\ x成分とy成分を別々に計算するだけである 大きさは\ √8^24^2}=√80}=4√5\ と計算してもよいが,\ うまくない 今後z成分も考慮したり,\ 数値が大きくなったりした場合,\ 計算が一気に面倒になる 2ab= (8,\ 4)=4 (2,\ 1)と考えると,\ 実質的に\ √2^21^2

この三角形の面積公式はなぜこうなるのですか Clear

ベクトルを使った三角形の面積の公式って Pq Pr Cos Qpr 2 Yahoo 知恵袋

 三角比による三角形の面積の公式{S=12absinθが元になる} これを,\ {sinθ\ →\ cosθ\ →\ 内積の定義}という流れでベクトルで表し,\ 整理すればよいsin²θcos²θ=1より本来sinθ={1cos²θ}\ だが,\ sinθ>0より\ sinθ={1cos²θ}\ である 内積の定義を適用し,\ 通分すると結局約分できる さらに,\ 成分表示にした後に整理する {S=0とすると,\ a₁b₂a₂b₁=0(平行条件b=kaの成分表示)}となる 面積を $2$ 通りの方法で表すことで、方程式を作ることができるんですね～。 ⇒参考「三角形の面積の求め方とは？sinやベクトルを用いる公式も解説！小学生から高校生まで」 スポンサーリンク 内心の座標を求める問題数学Ⅱベクトルの平行条件，垂直条件 3点が一直線上にある条件 → 携帯版は別頁 == 三角形の重心,内心,外心,垂心 (ベクトル,三角関数) == このページで解説する内容 各々その項目をクリックすれば解説にジャンプします 原点を O とし， ABC の頂点の位置

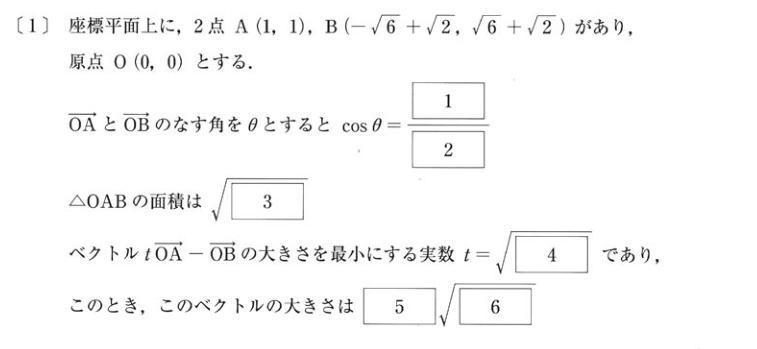
平面ベクトルの内積 三角形の面積 ベクトルの長さの最小問題です 大学入試数学問題の解説 解答

48s96ub7b0z5f Net Kuukan Bekutoru Menseki

3．多角形の重心 n角形の物理的重心 は、頂点の位置ベクトルを とすると、 で与えられる。また、幾何的重心については、対角線により分割された幾つかの図形の重心を質点とした面積を重さとみた質量中心を考えればよい。 数学 空間ベクトル 次の図形の面積を求めよ 3点A(1,2,3)B(1,0,3)C(1,2,3)を頂点とする三角形 θを求めてからABsinθ×ACかなと、思ったんですが計算が出来ませんでした。義や合同，面積を定義する．x4 では，図形の基本となる双曲3角形について考える．双 曲3角形の面積や正弦定理・余弦定理の証明，ユークリッド幾何における3角形との違い について考える．x5 では，直角多角形を考える際に重要となるランバートの4角形を紹 3

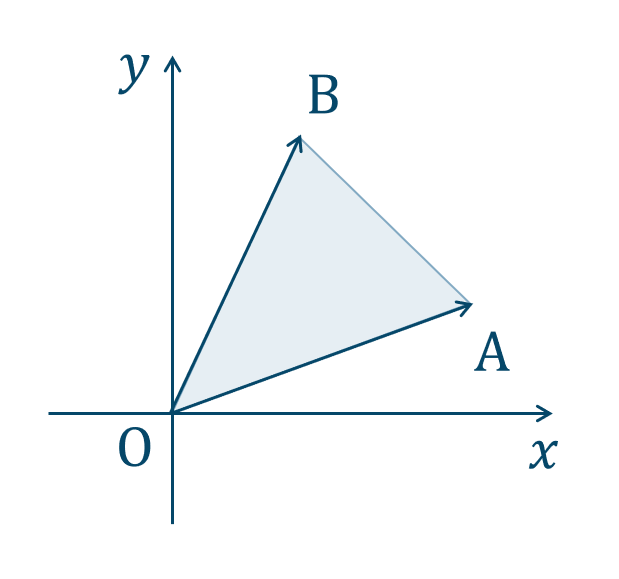
数学ｂ ベクトルを用いた三角形の面積の求め方とコツ ページ 2 教科書より詳しい高校数学

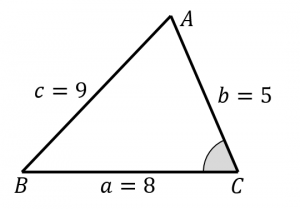
三角形の面積を３辺の長さから求める２つの方法 具体例で学ぶ数学

 面積 座標平面上の三角形の面積に関わる問題です。 直線の方程式に慣れ親しんで下さい。 式を見てどのような直線を表すかを瞬時に分かることが大切です。 1． B (滋賀大) 3点O, A, B を頂点とする OABの面積を，直線 が2等分しているときの の値を求めよS formula (1) area S = √s(s−a)(s−b)(s−c) s= (abc) 2 T r i a n g l e b y H e r o n ′ s f o r m u l a ( 1) a r e a S = s ( s − a) ( s − b) ( s − c) s = ( a b c) 2 お客様の声 アンケート投稿 よくある質問 四角形を2つの三角形に分けてから各三角形の面積 S 1, S 2 を ヘロンの公式 を使って求め、それらを合計することで四角形の面積を求めることができます。 ヘロンの公式 3辺の長さ a, b, c が分かっている場合、その三角形の面積 S は S = s ( s − a) ( s − b

1

ベクトルの三角形の面積公式を超わかりやすく説明した 理系ラボ

三角形の面積を二等分する 垂線 理系男子の独り善がり

ベクトルの公式一覧 計算 内積 三角形の面積 共線条件 理系ラボ

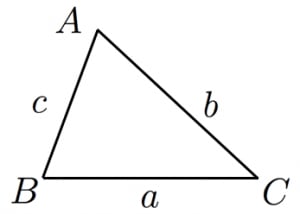
Sinを用いた三角形の面積公式 高校数学の美しい物語

同一直線上にない平面上の３点でできる三角形の面積 ベクトル内積を用いて 高校数学 身勝手な主張

ベクトルの公式一覧 計算 内積 三角形の面積 共線条件 理系ラボ

ベクトルを用いた三角形の面積公式3種類 数学の庭

三角形の面積を求める公式７選 高校数学のまとめにどうぞ

Excelを使った数値計算ツールsuitexl

小学校の算数の図形問題をベクトルで解く 東大合格コム

三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ

ベクトルを使った三角形の面積の公式は外積ですか 二次元 内積または外 Yahoo 知恵袋

ベクトルの三角形の面積の公式について 高校数学の勉強法 河見賢司のサイト

応用 ベクトルの等式と三角形の面積比 なかけんの数学ノート

平面上の異なる３点を頂点とする三角形の面積 身勝手な主張

２０１６年 東大数学 理系第３問 空間図形 ベクトル 三角形の面積 オンライン受講 東大に 完全 特化 東大合格 敬天塾

3点が与えられた三角形の面積 点と直線の距離 Gutugutu3030

数b ベクトル 三角形の面積 Youtube

三角形の面積の求め方とは Sinやベクトルを用いる公式も解説 小学生から高校生まで 遊ぶ数学

ベクトルによる三角形の面積公式 ゼロからわかるベクトル第13回 Youtube

三角形の面積のベクトル 成分を用いた公式 高校数学の美しい物語

高校数学ｂ 平面ベクトル 公式一覧 内分 外分 面積 学校よりわかりやすいサイト

三角形の面積の最小 内分のベクトルの問題です 大学入試数学問題の解説 解答

数学ｂ ベクトルを用いた三角形の面積の求め方とコツ 教科書より詳しい高校数学

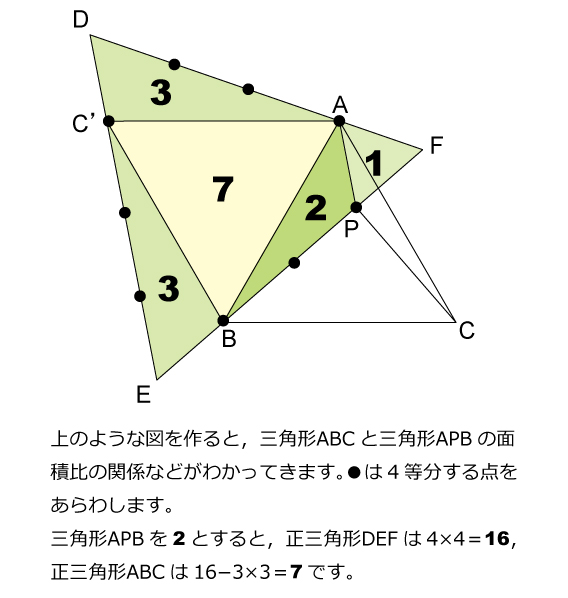
灘中解説速報 19年第9問 正三角形と面積比 算数星人のweb問題集 中学受験算数の問題に挑戦

ベクトルを用いた 三角形の面積の公式 数学b By Okボーイ マナペディア

三角形の面積の公式 怜悧玲瓏 高校数学を天空から俯瞰する

平面ベクトル 三角形の面積 オンライン無料塾 ターンナップ Youtube

四面体の体積

高校数学b 三角形の面積のベクトル表示 成分表示とその証明 受験の月

三角形の面積比 京極一樹の数学塾

数学 面積比と線分比をシッカリわかると チェバの定理を深く理解できるよ 平面図形 中学数学 高校数学 行間 ぎょうのあいだ 先生

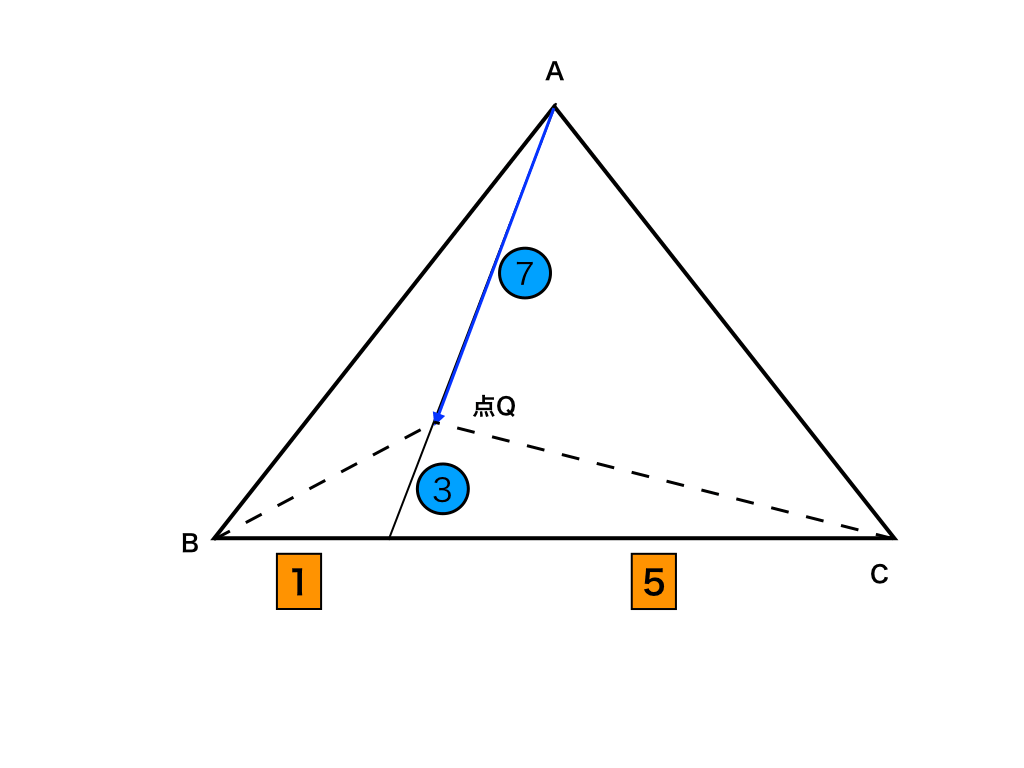
ベクトルの和で表された式から点pの位置を求める方法を解説

ベクトルを用いた三角形 平行四辺形の面積の公式と求め方 高校生向け受験応援メディア 受験のミカタ

6 柱と梁の断面形と幾何学

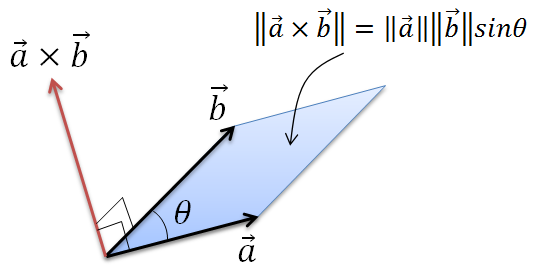
３点からなる三角形の面積を求める イメージングソリューション

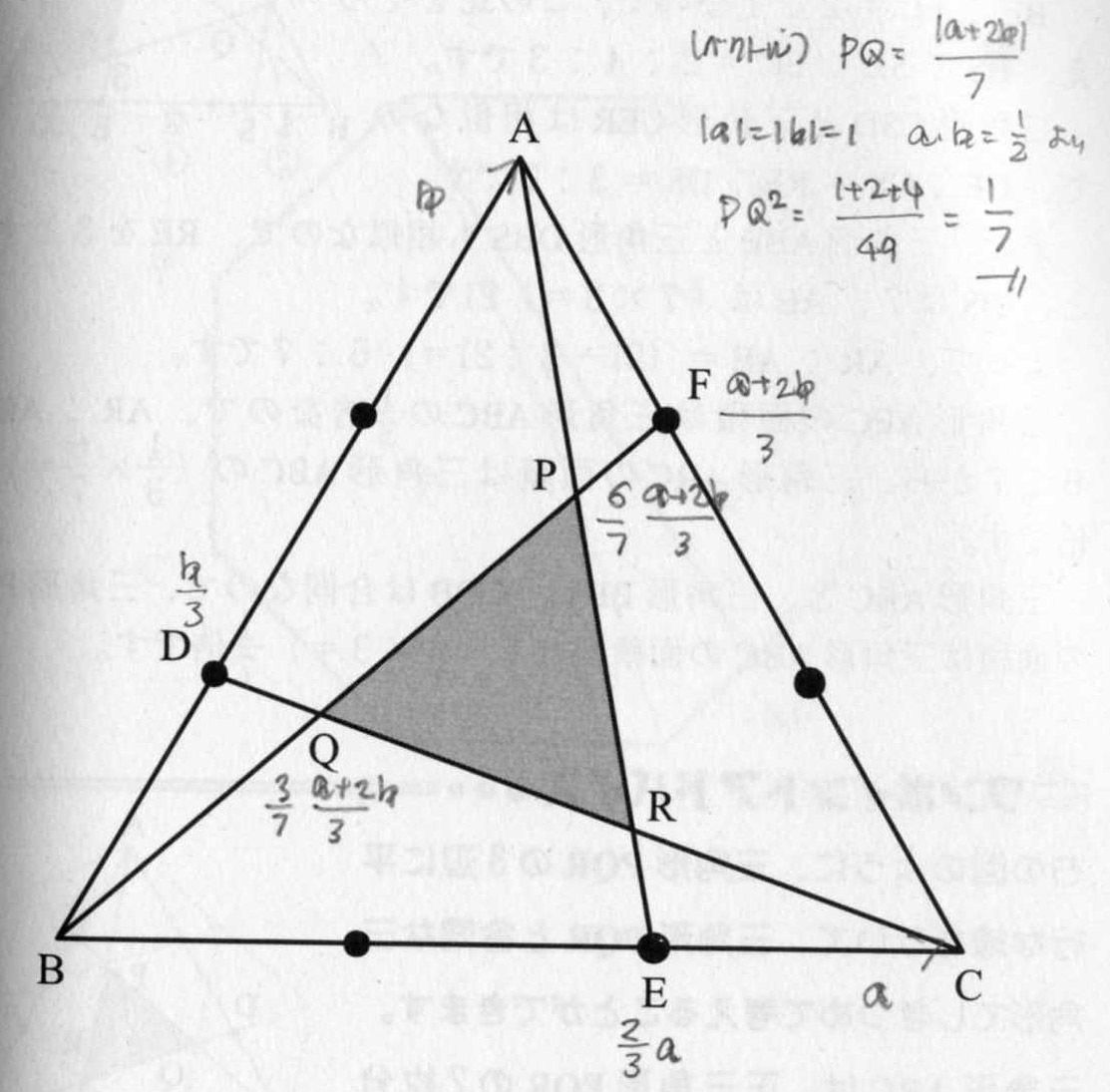
小学校の算数の図形問題をベクトルで解く 東大合格コム

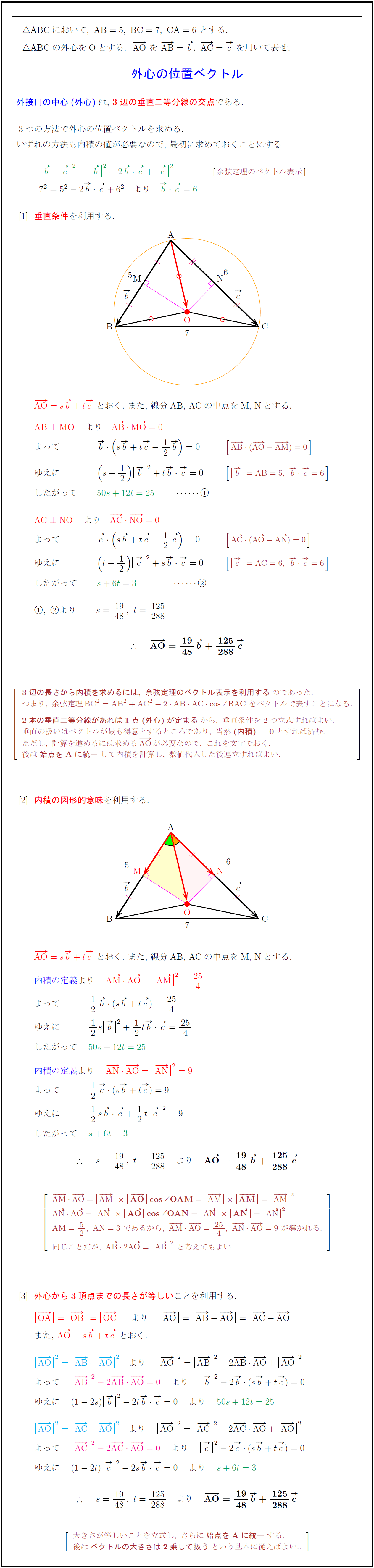
高校数学b 三角形の外心の位置ベクトル 受験の月

三角形の面積 証明 受験数学って暗記 仮 高校受験 大学受験 楽天ブログ

大学入試に必要な三角形の面積について 楽しく学ぶ大学受験数学

ベクトルを使った三角形の面積 数学の偏差値を上げて合格を目指す

1

勉強しよう数学 三角形の面積をベクトルで分解して計算する

三角形の面積 ベクトル利用 大学受験の王道

48s96ub7b0z5f Net Bekutoru Menseki

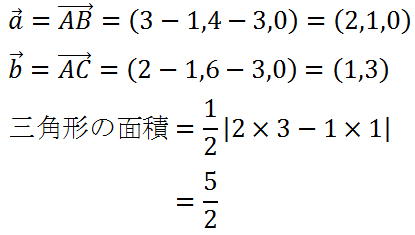
３点からなる三角形の面積を求める イメージングソリューション

勉強しよう数学解答集 ３次元の立体上の三角形の面積を平面上の三角形の逆射影で計算する

ベクトルによる三角形の面積の求め方 公式や証明 計算問題 受験辞典

三角形の面積の求め方とは Sinやベクトルを用いる公式も解説 小学生から高校生まで 遊ぶ数学

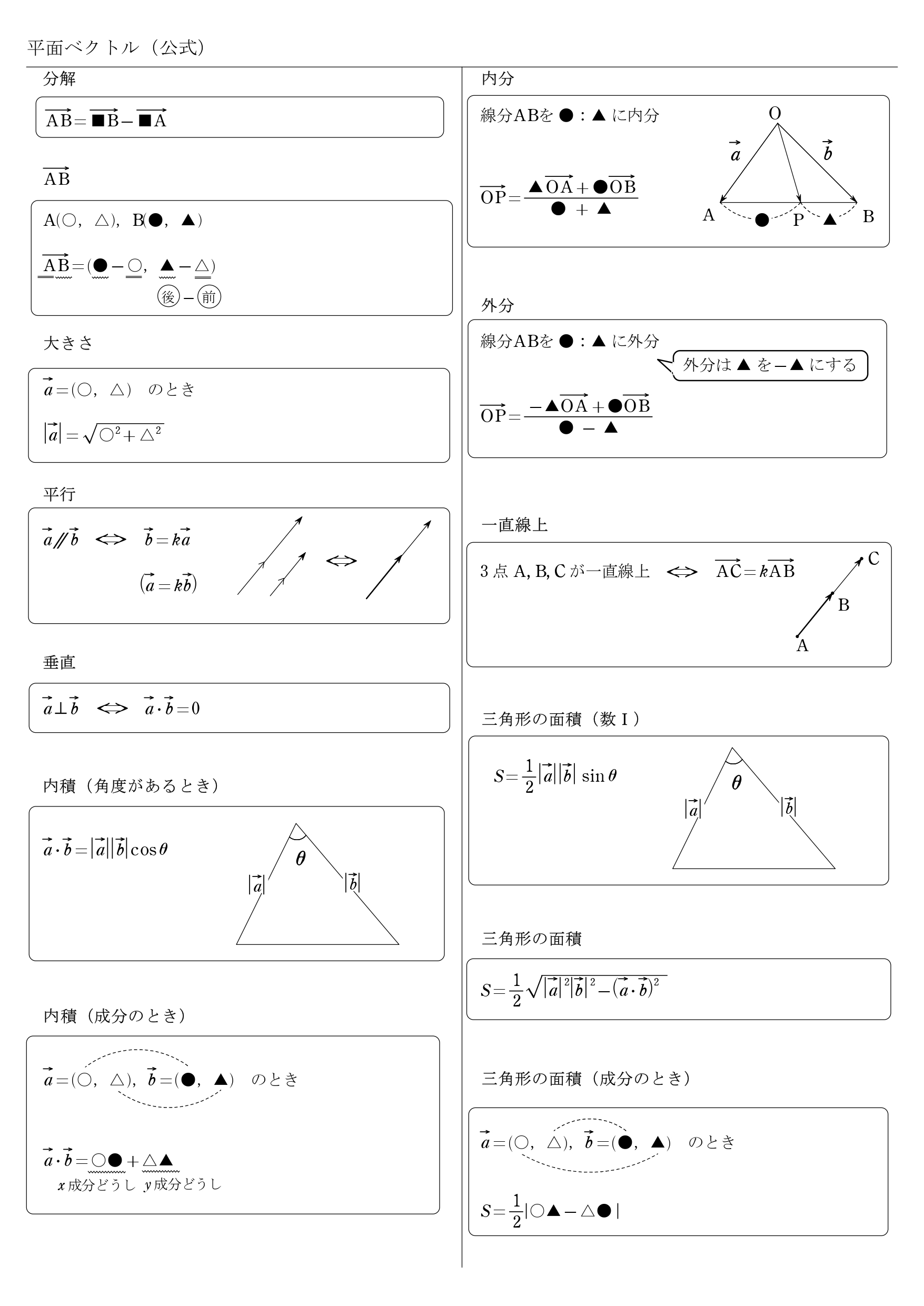
高校数学ｂ 平面ベクトル 公式一覧 内分 外分 面積 学校よりわかりやすいサイト

ベクトル編 ベクトルで色々な図形を表現する 大学1年生もバッチリ分かる線形代数入門

ベクトルの三角形の面積を求める問題ですが なぜ1 2 1 1 3 4 13 Clear

三角形の重心の性質 思考力を鍛える数学

多角形の面積を求める Javascript版

三角形の内部の点と面積比の公式の証明 ゼロからわかるベクトル第32回改訂版 Youtube

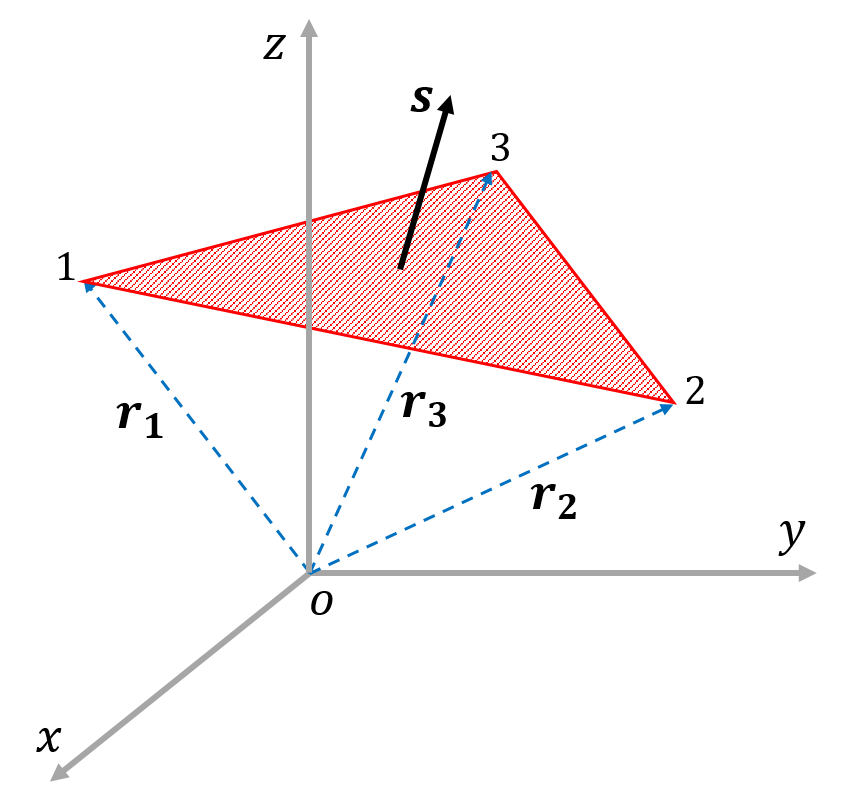
三角形の面積 科学技術計算ツール

三角形 Wikipedia

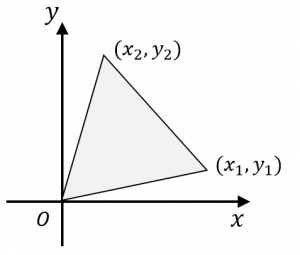
座標平面上で三角形の面積を計算する公式 具体例で学ぶ数学

ベクトルにおける三角形の面積の公式の導出とコツ 高校数学の知識庫

三角形の面積のいろいろな表し方 思考力を鍛える数学

３点からなる三角形の面積を求める 画像処理ソリューション

倍横距法を用いて多角形の面積を求める方法

高校数学でよく使う三角形の面積公式まとめ おいしい数学

Studydoctor空間上での三角形の面積 数ｂ Studydoctor

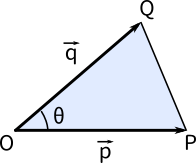
数bベクトル ベクトルで作る三角形の面積を導出する Mm参考書

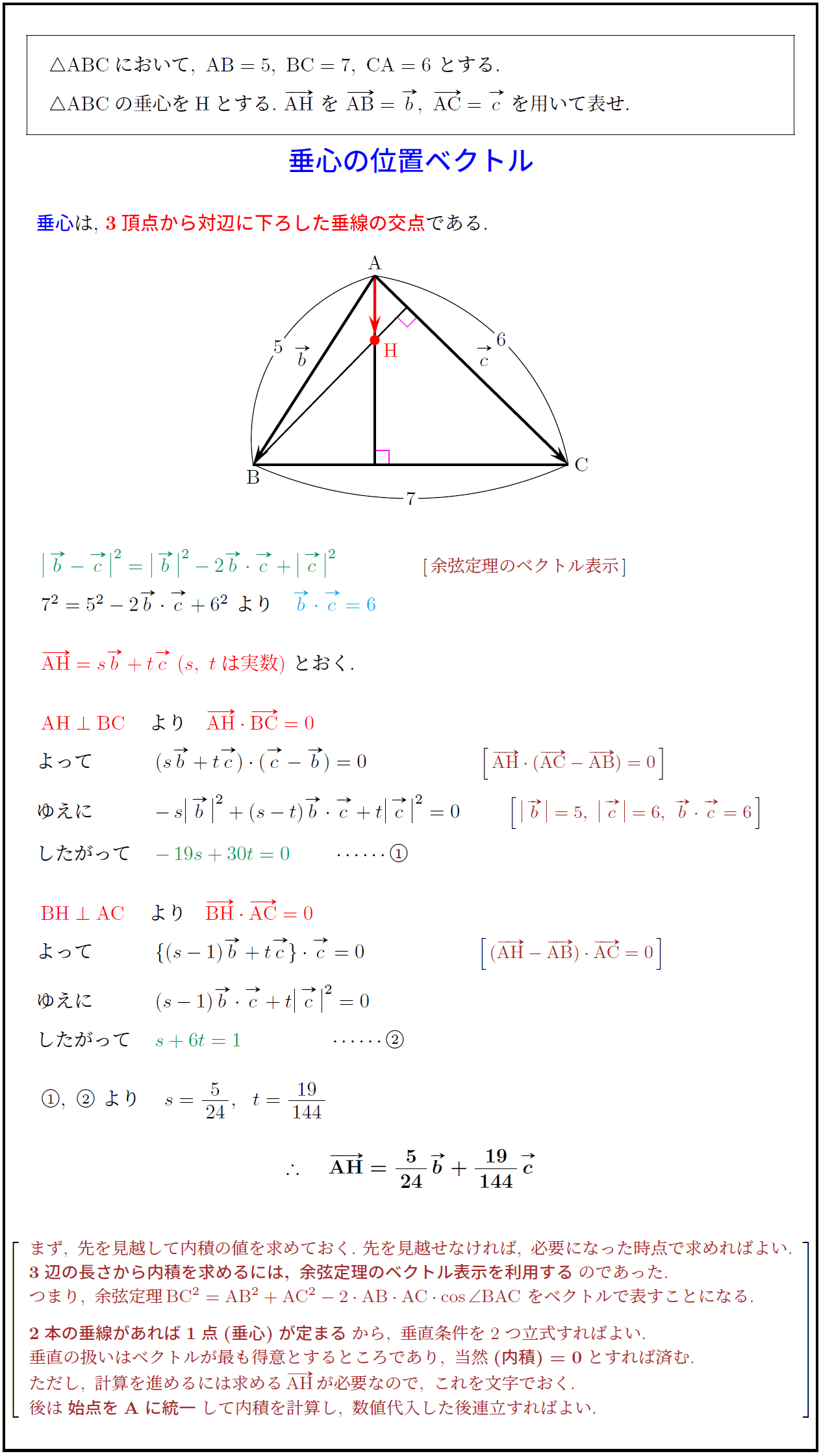
高校数学b 三角形の垂心の位置ベクトル 受験の月

三角形の面積の求め方とは Sinやベクトルを用いる公式も解説 小学生から高校生まで 遊ぶ数学

高校数学b ベクトル表示の三角形の面積公式 映像授業のtry It トライイット

平行四辺形の面積 ベクトルでの公式 理数系無料オンライン学習 Kori

Studydoctorベクトルと三角形の面積公式 数ｂ Studydoctor

Q Tbn And9gct71t318twmynw63dxmqoj5dsomuiz6o0rnzjk6hursgayaq9 L Usqp Cau

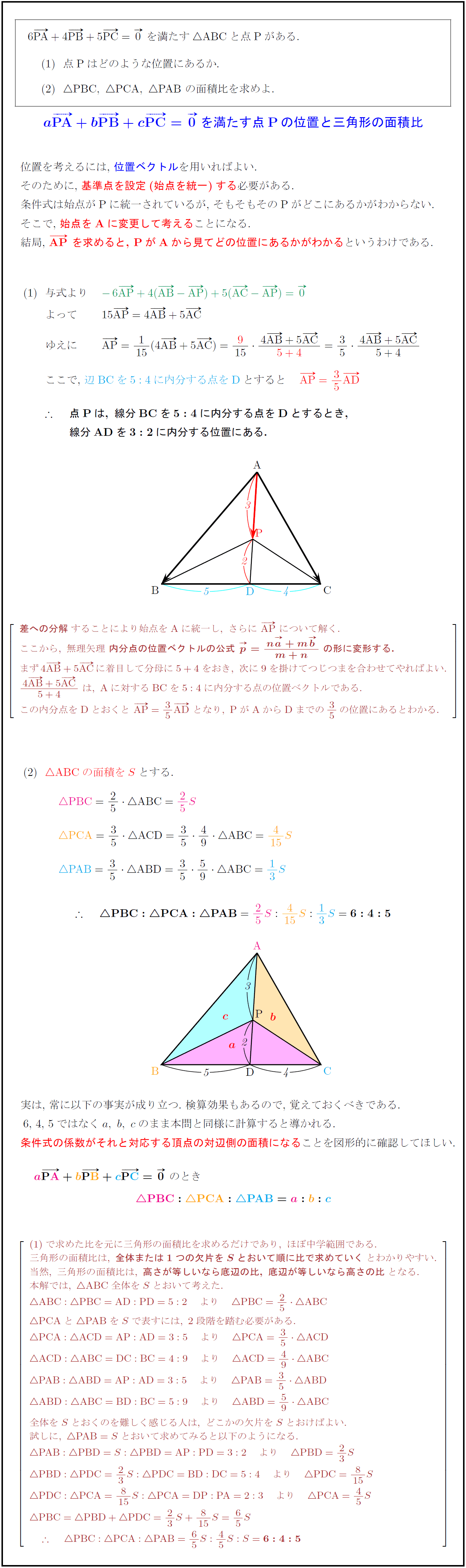
高校数学b Apa Bpb Cpc 0を満たす点pの位置と三角形の面積比 受験の月

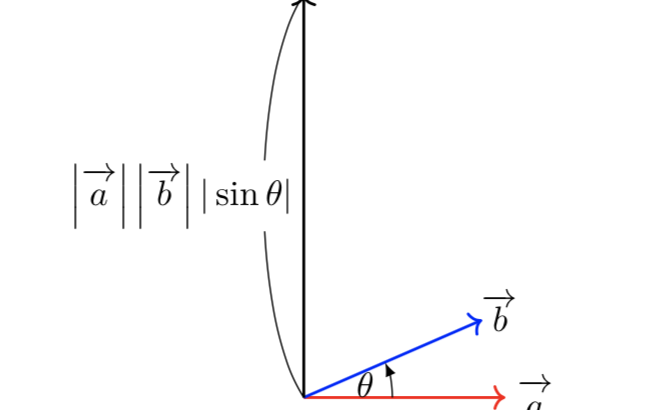
ベクトルの外積の公式やその覚え方とは 高校範囲で役立つ場面についても解説 東大医学部生の相談室

ベクトルを使った三角形の面積公式 Youtube

平面上の異なる３点を頂点とする三角形の面積 身勝手な主張

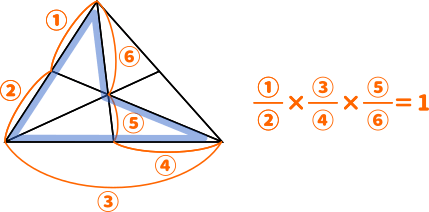
数a図形の性質 三角形内の内分点をチェバ メネラウスを使って求める 九州大 Mm参考書

ベクトル方程式による面積比の問題と解き方

空間ベクトルとは 内積 面積などの公式や問題を解くコツ 受験辞典

外積を使って解く入試問題例 東大落ちの受験勉強法

基本 三角形の重心の位置ベクトル なかけんの数学ノート

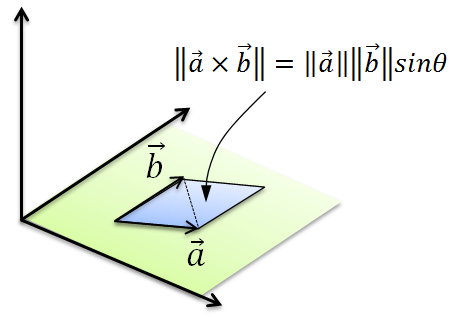
３点からなる三角形の面積を求める イメージングソリューション

平面ベクトル 三角形の面積比 Cupuasu クプアス

三角形の面積の求め方まとめ 数学の偏差値を上げて合格を目指す

高校数学b ベクトル表示の三角形の面積公式 映像授業のtry It トライイット

三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ

数学b 位置ベクトルと三角形の面積比 日本大学19 高校生 数学のノート Clear

必ず押さえておきたいベクトルの問題その１ Part2 高校数学の知識庫

ベクトルを使った三角形の面積の練習問題 中学数学 高校数学のサイト ときどき大学数学

高校数学でよく使う三角形の面積公式まとめ おいしい数学

Incoming Term: ベクトル 3角形の面積,