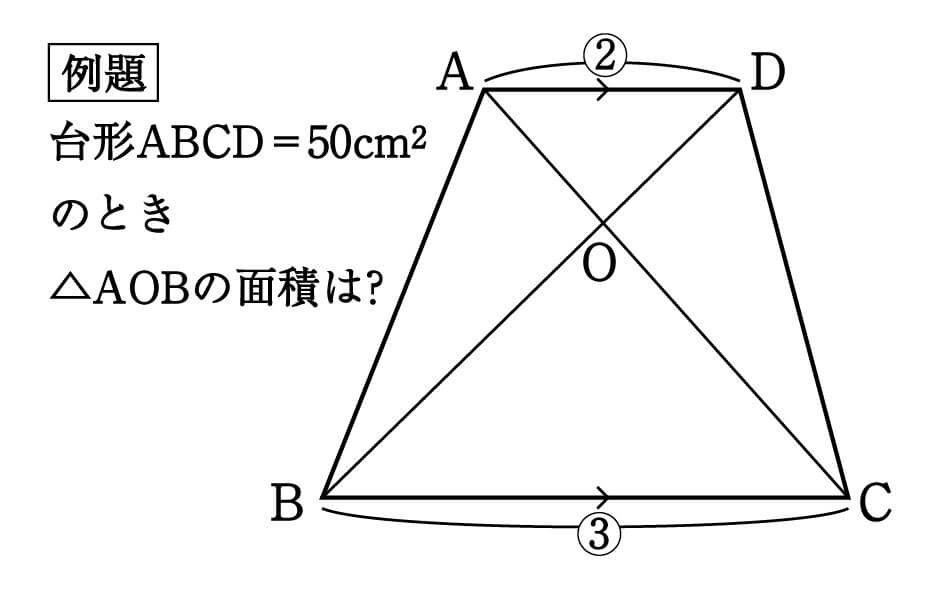
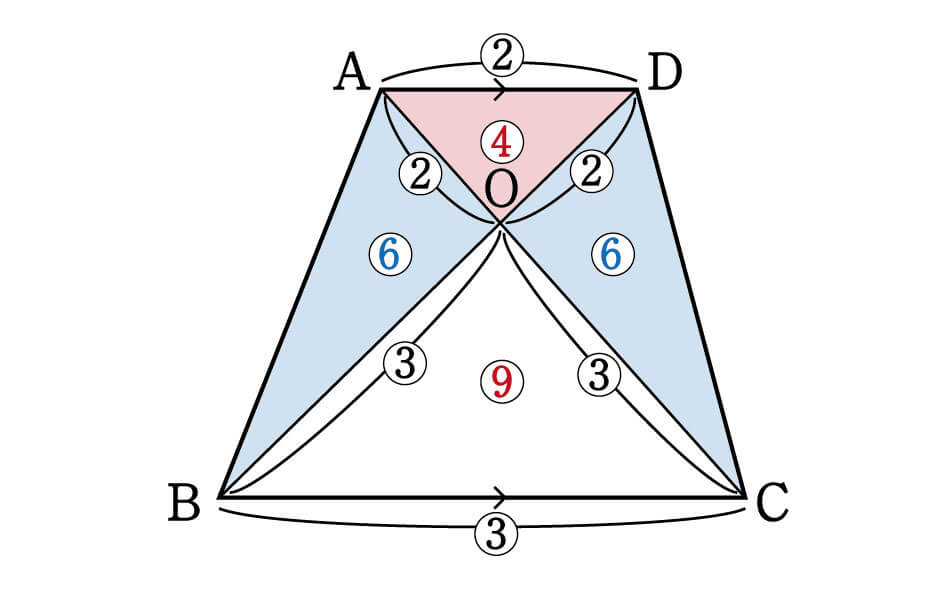
台形の面積 ガラスの面積を出すのに使いました。 助かりました。 利用させてもらって、助かってます。 工事現場。 顧客、住民さんへ計算式等の説明も出来るので助かってます。 面積から逆算できる上辺・下辺・高さがほしいです。 (組み合わせ円錐台の側面積を計算する Runcated cone 円錐台の側面積は π × ( r1 r2 )× √(( r1 r2 ) × ( r1 r2 ) 高さ × 高さ ) で求めることができます。 底面半径 (r1) : 上面半径 (r2) : 高さ (h) : 側面積 : 円錐台の体積 円錐台の表面積 円錐台の側面積 使用しているスクリプトの特性から、特に少数点以下 台形abcdがあり、上底adと下底bcの比は2:3です。 台形の面積が50cm 2 であるとき、 aobの面積はいくつでしょうか? という問題です。 問題文には‟面積比"という言葉が使われていませんが、2つの異なる図形の面積を比べる問題なので、これも面積比のパターンの1つです。
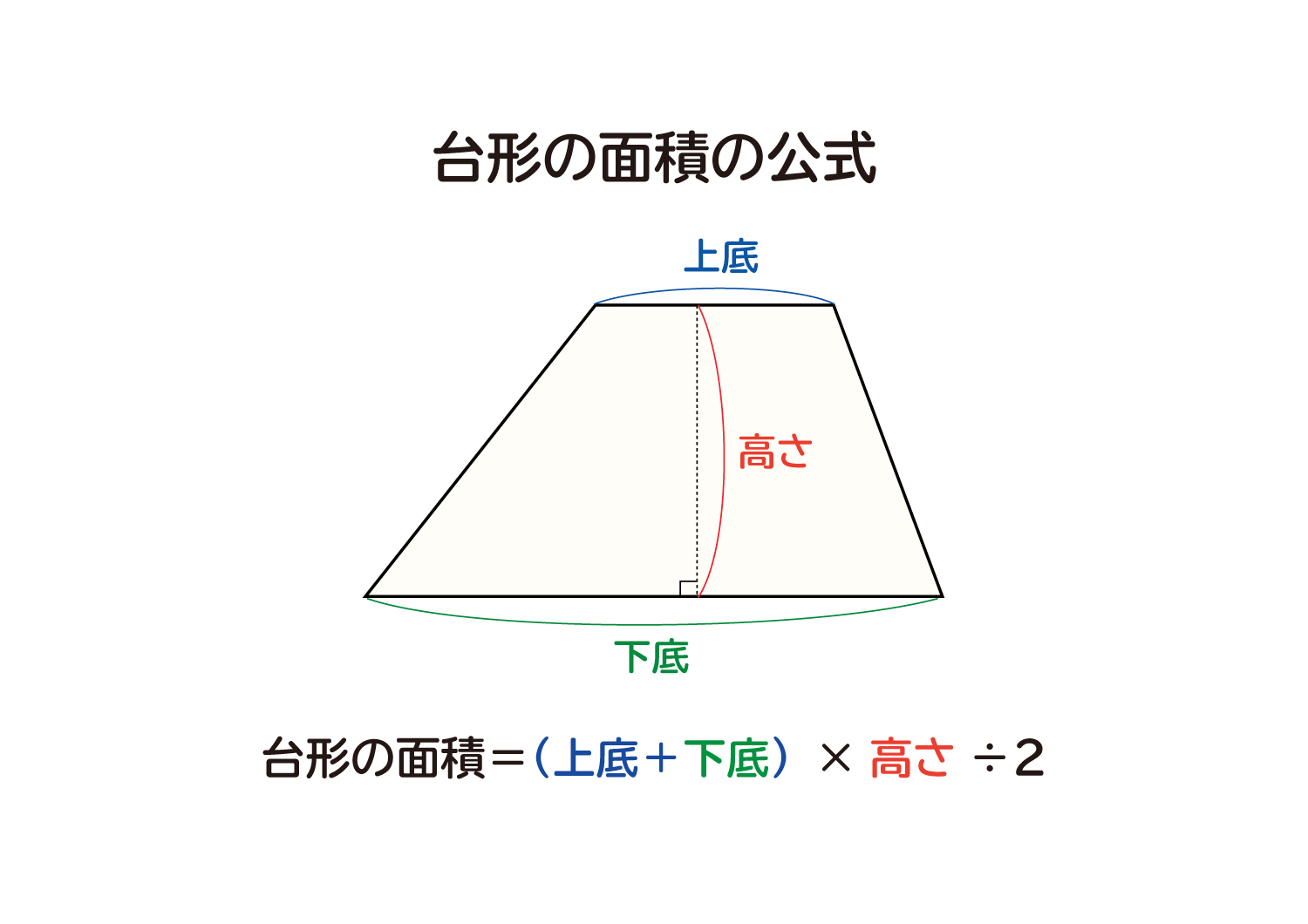
なぜ 台形の面積は 上底 下底 高さ 2 なのか を説明します おかわりドリル
台形面積
台形面積- 台形の面積は「復活」なの? 学校の授業の基準になる学習指導要領の改訂論議が、大詰めを迎えています。 そんななか、新聞で「台形の面積復活」という見出しがおどりました。 一読して、「ああ、『ゆとり教育』で消えた『(上底+下底)×高さ÷2台形abcdから、 pabと pcdの面積を引く。 台形abcdの面積 (1218)×8÷2=1 pabの面積 図で赤い線で示した部分がpが通った道のり2x よってpb=2x18 これが高さ ab=18 が底辺である。 面積 18×(2x18)÷2=18x162 pcdの面積 高さ pc=262x 底辺 cd=12 面積 12×(262x)÷2=x
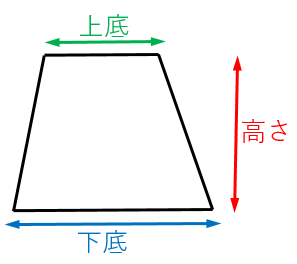



台形の面積を求める公式 具体例で学ぶ数学
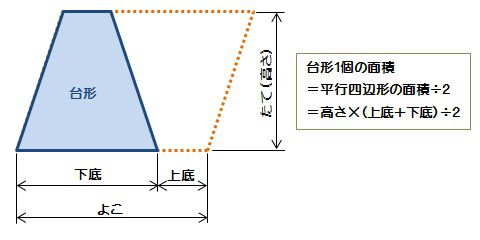
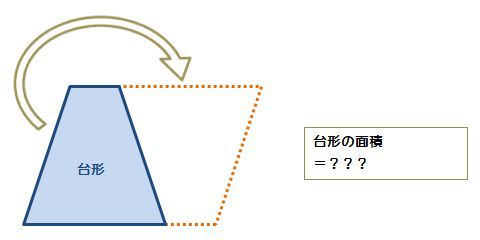
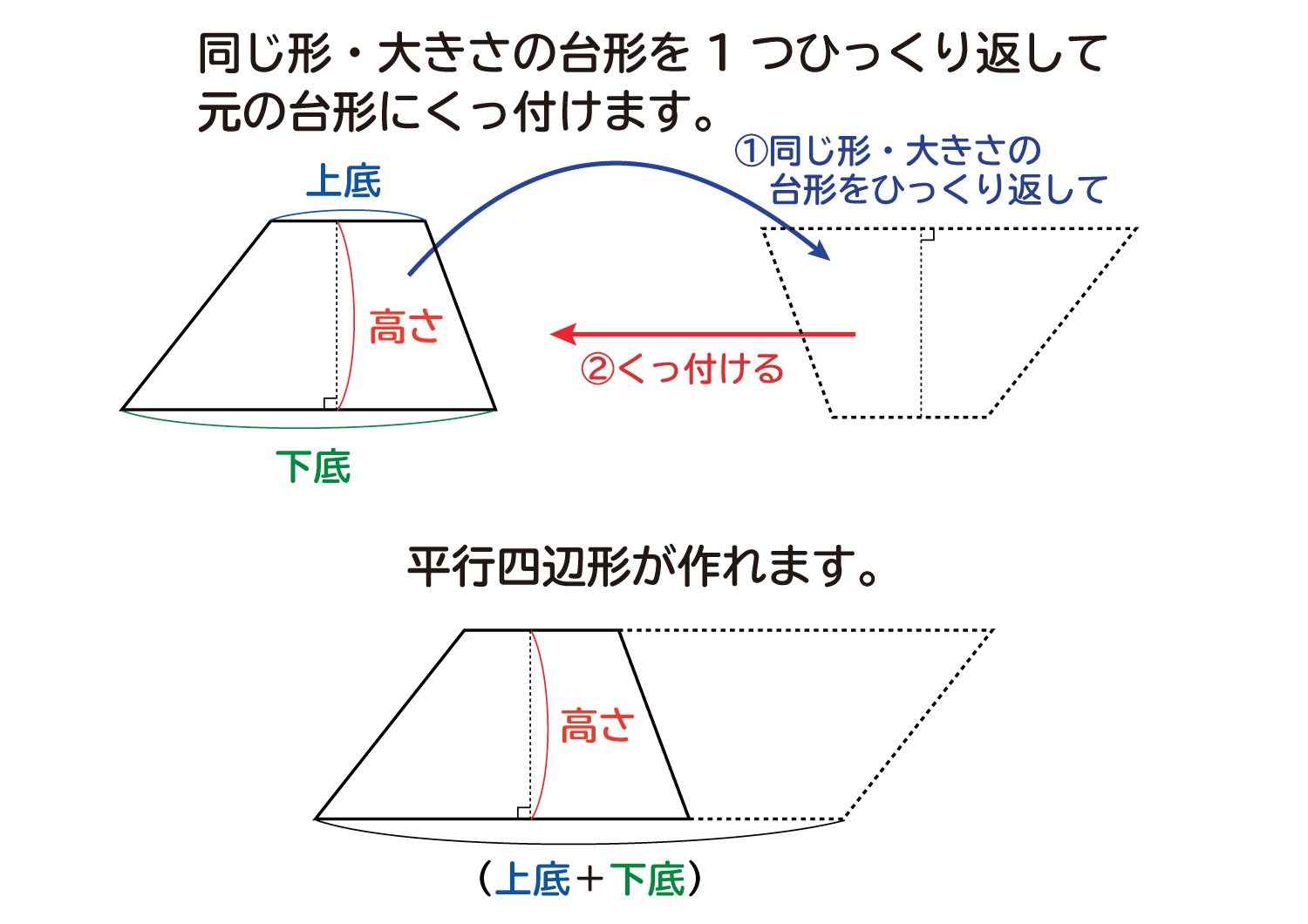
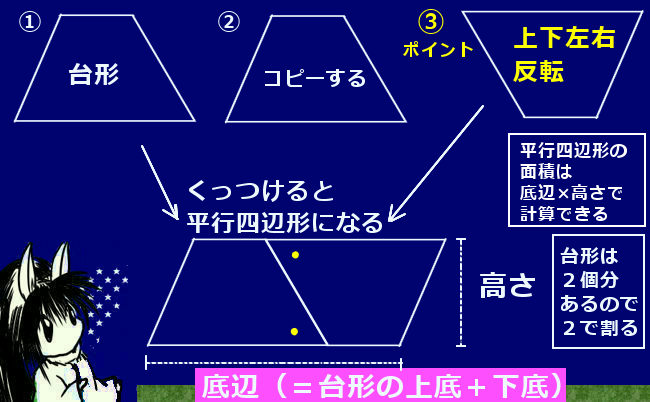
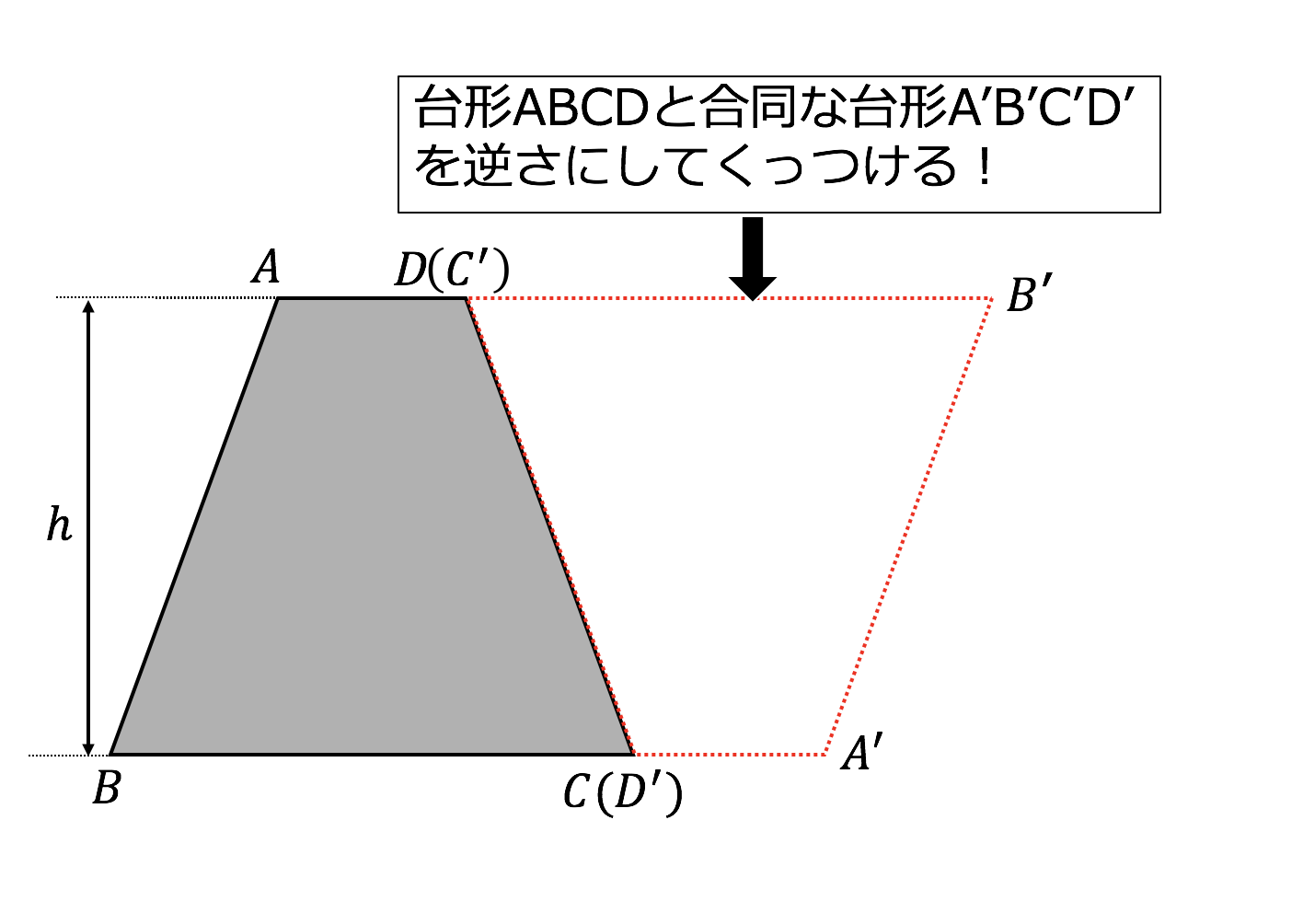
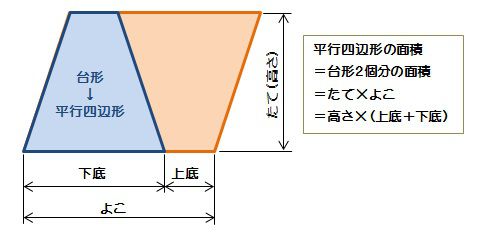
台形断面の等流計算 開水路の等流計算には、次のマニングの公式がよく用いられる。 (式-2) 補足 (上底+下底)×高さ÷2 で上底= として整理する。 ここで、各記号は次のことを示している。 n:粗度係数(水路壁面、底面の粗さを示す値で、水路の台形2個を合体させた平行四辺形の面積は、高さ×(上底+下底) 求めたいのは台形1個の面積 こうなります。つまり、 台形1個分の面積=平行四辺形の面積÷2 と考えればいいのです。 なので、 台形の面積=(上底+下底)×高さ÷2 となるのです♪ 台形の計算問題 計算問題①「台形の面積と角度を求める」 計算問題②「台形の高さを求める」 計算問題③「台形の面積比から辺の比を求める」 台形とは? 定義 台形とは、 少なくとも 組の向かい合う辺がお互いに平行であるような四角形 のこと
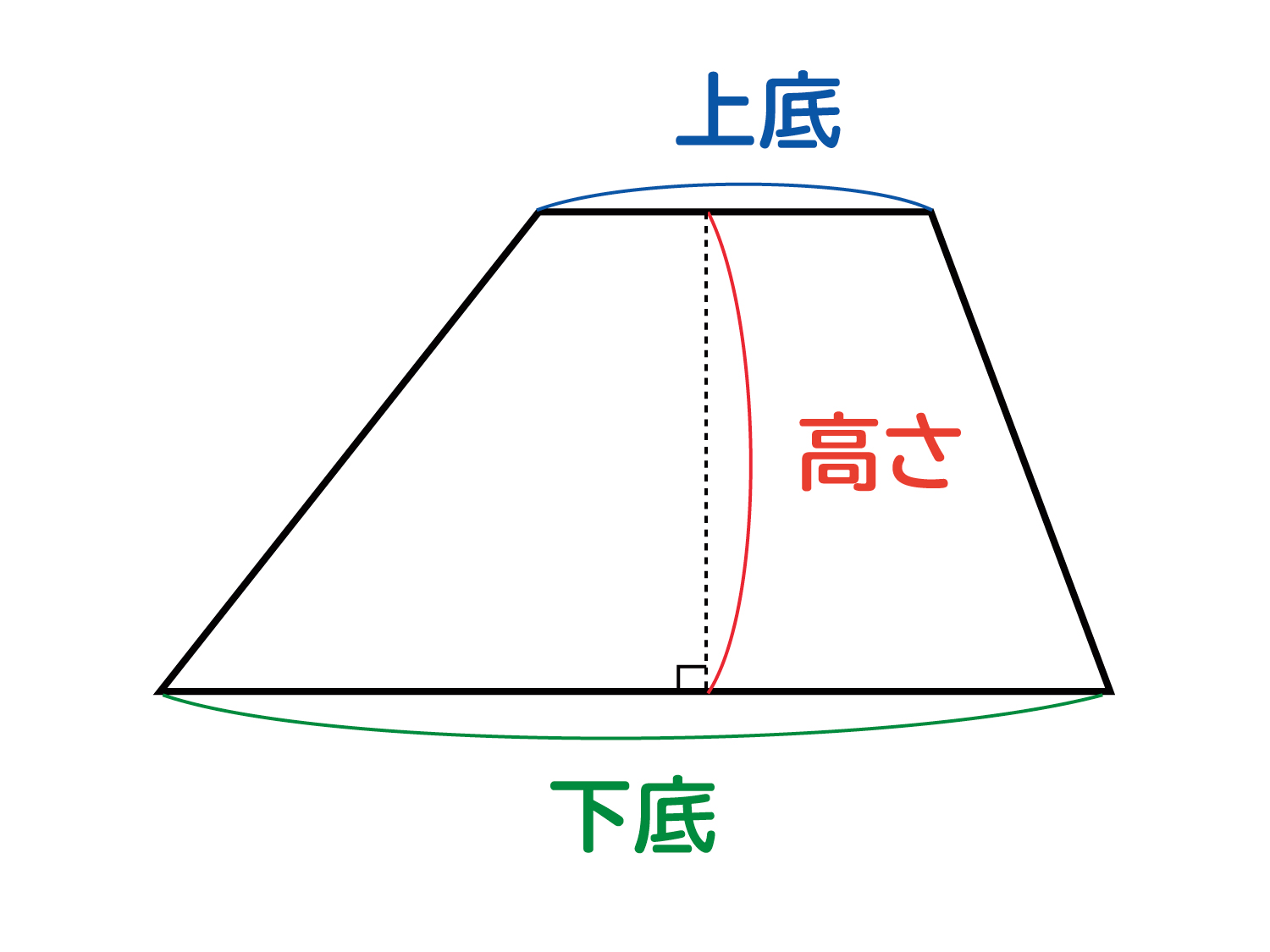
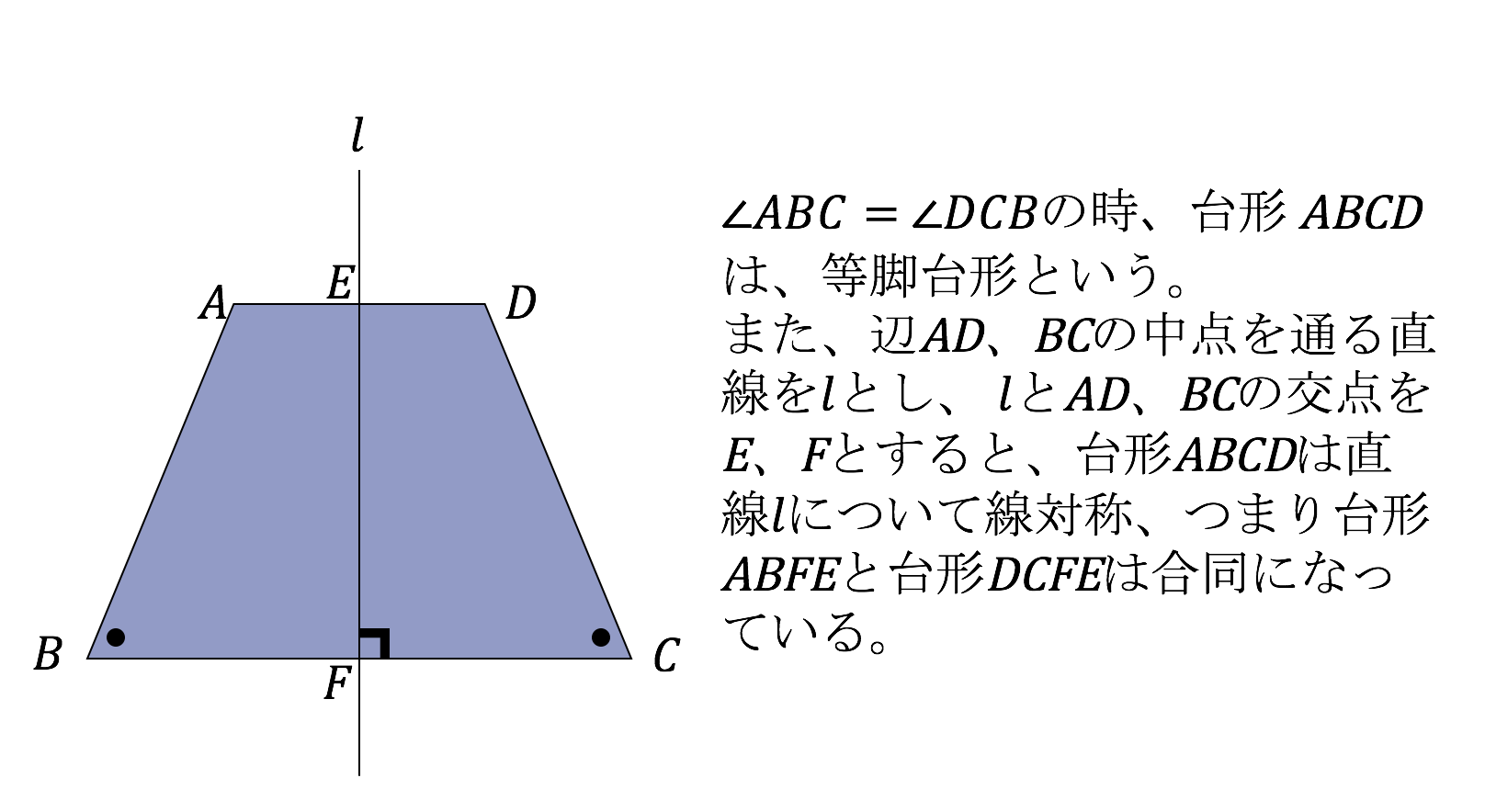
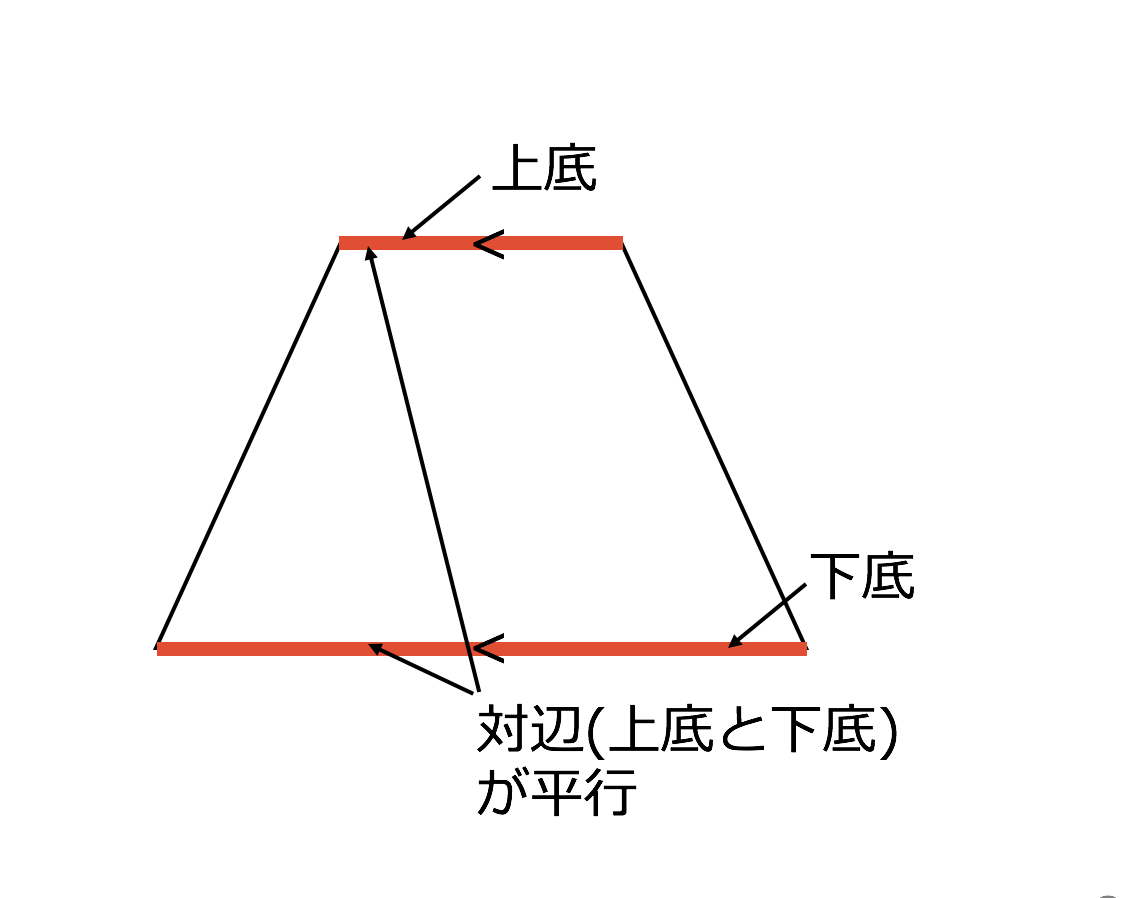
台形(だいけい、米 trapezoid 、英 trapezium )は、四角形の一部で、少なくとも一組の対辺が互いに平行であるような図形である。 平行な2本の対辺を台形の底辺といい、そのうち一方を上底(じょうてい)、他方を下底(かてい)とよぶ。また、もう一組の対辺を台形の脚(きゃく)とよぶ。既習の面積の公式を基に、三角形、平行四辺形、ひし形及び台形の面積を求める公式を逭んで 見出そうとしている。 (関心・意欲・態度) 既習の面積の公式を基に、三角形、平行四辺形、ひし形及び台形の面積を工夫して求めたり、 公式にまとめたりできる。 (数学的な考え方) 三角形、平円錐台の体積 円錐台の表面積 円錐台の側面積 使用しているスクリプトの特性から、特に少数点以下の計算結果に誤差が出る場合があるようです。参考としてご覧ください。 90種類を超す各種計算がある『目次』へ おすすめサイト・関連サイト トップページ・ Home 90種類を超す各種計算が
小学5年生の算数 四角形の面積台形・ひし形ほかの問題プリントを無料ダウンロード・印刷 (プリント5枚) 小学5年生の算数 正多角形(概念や作図) 問題プリント 小学5年生の算数 正多角形(概念や作図)の問題プリントを無料ダウンロード・印刷 (プリント4枚) 小学5年生の算数 円台形の面積=(上底下底)×高さ÷2ですね。 平行な2つの辺のうち、どちらを上底、下底としてもよいので、 4と6が入れかわっていても間違いではありません。 ただし、学校によっては決められた順番どおりに式を書いていないと 減点する場合があります台形近似の考え方 S = ∫ a b f (x) d x S=\displaystyle\int_a^bf(x)dx S = ∫ a b f (x) d x を求める問題を考えます。 定積分の値を台形の面積(の和)で近似してみましょう。数値積分(計算が難しい定積分の値を近似的に求める)が主なモチベーションです。入試では
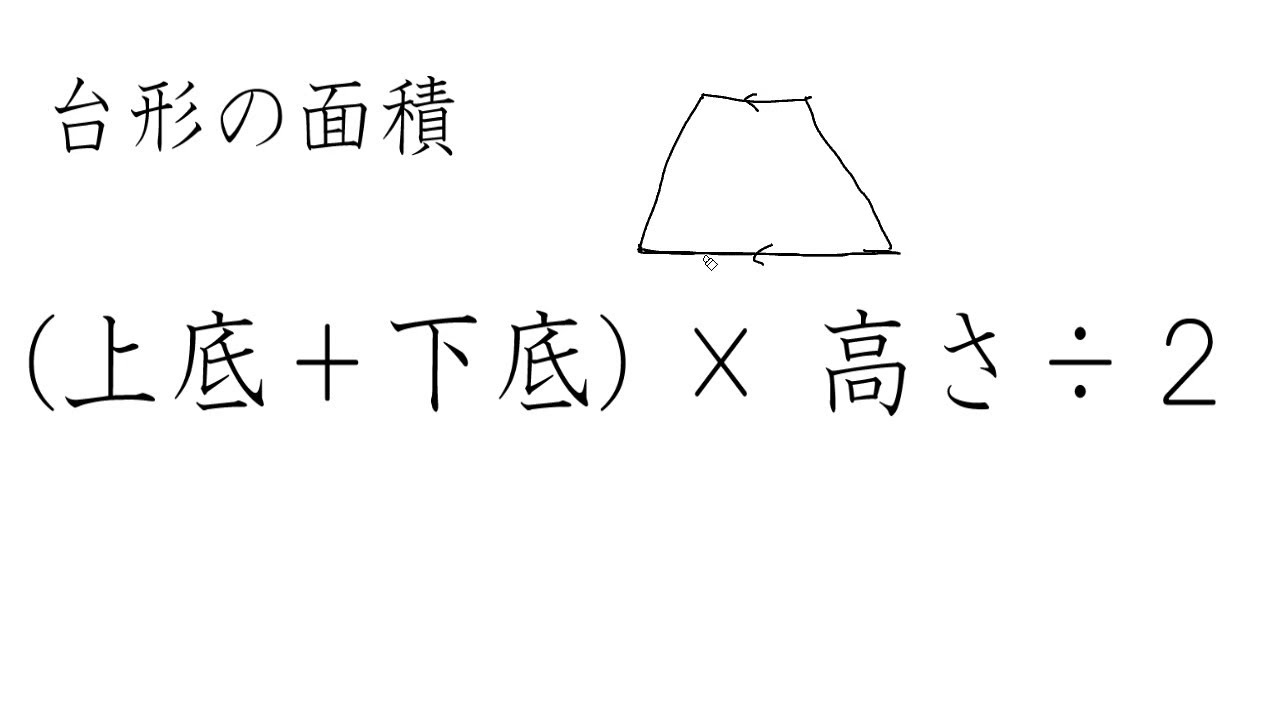



台形の面積の公式 Youtube
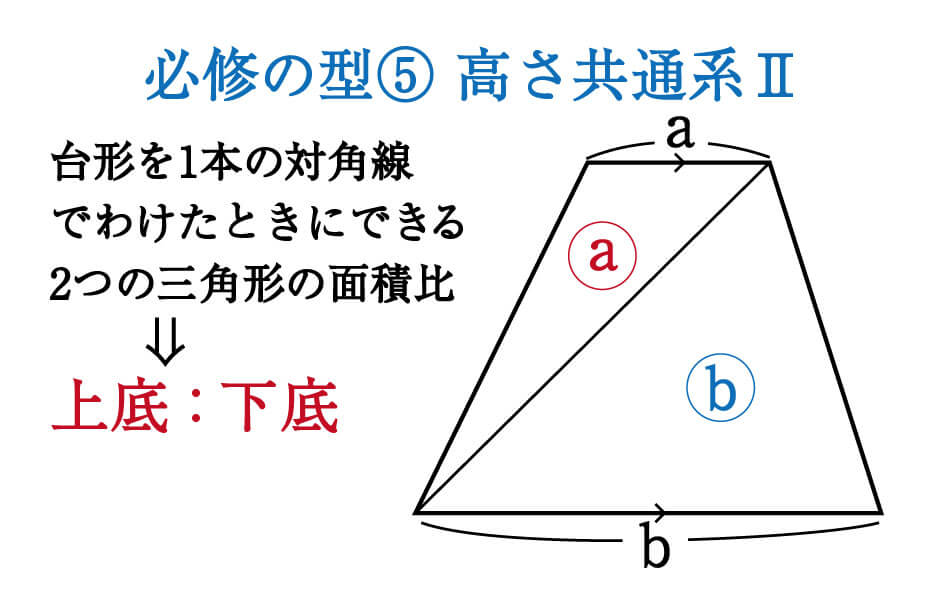



数学 対角線の入った台形 一角共有の三角形 面積比 集中特訓 6 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学 > 図形 > 円錐台の体積と表面積を計算する公式と証明 最終更新日 図のような円錐台について、 体積は、 V = 1 3 π h ( a 2 a b b 2) 側面積は、 S L = π ( a b) ( a − b) 2 h 2 表面積は、 S 台形の体積の求め方 を教えてほしい。 そう、きかれることが結構ある。 正直ドヤ顔で、 台形の体積はね・・・ って答えそうになる。 だけれども、 そもそも台形に体積はないんだ! 台形は平面図形だからね。 台形の面積なら求められるけど、体積は無理数学において、台形公式(だいけいこうしき、英 trapezoidal rule )もしくは台形則(だいけいそく)は定積分を近似計算するための方法、すなわち数値積分のひとつである。 これはニュートン・コーツの公式の1次の場合である。 被積分関数を区分線形関数で近似し、台形の面積の公式に帰着さ



台形の面積 算数の公式覚えてますか




台形の面積の公式 小学生に教えるための分かりやすい解説 数学fun
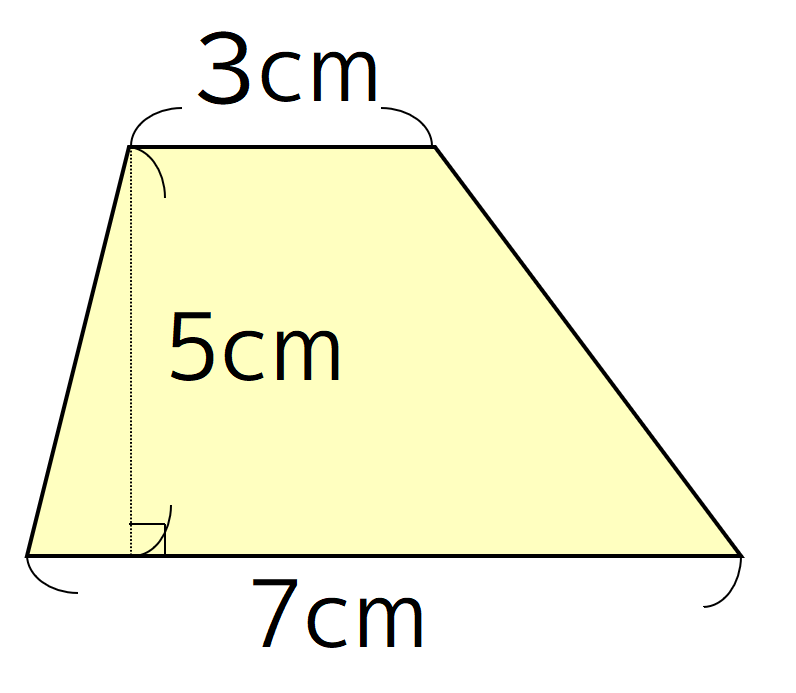
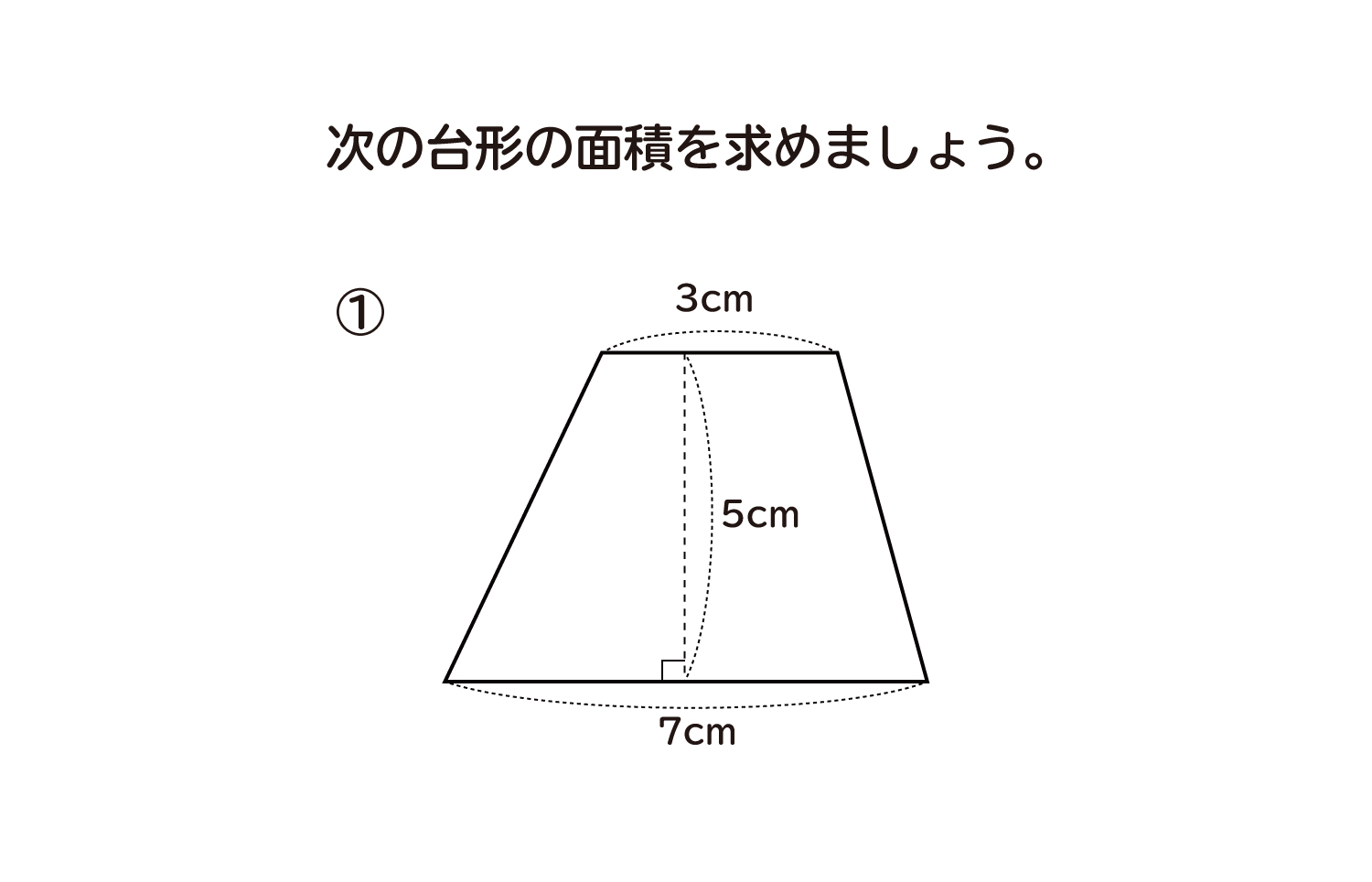
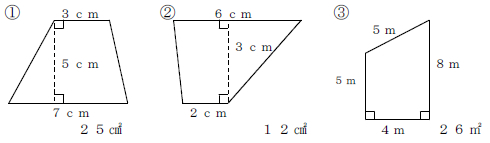
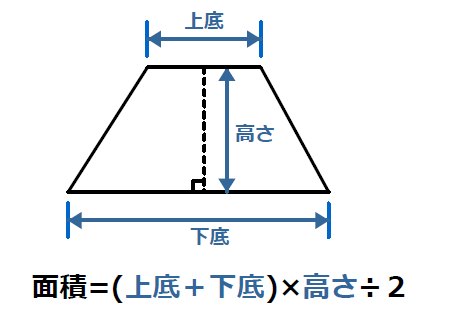
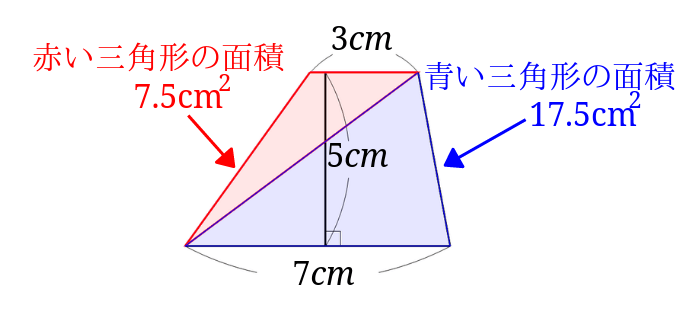
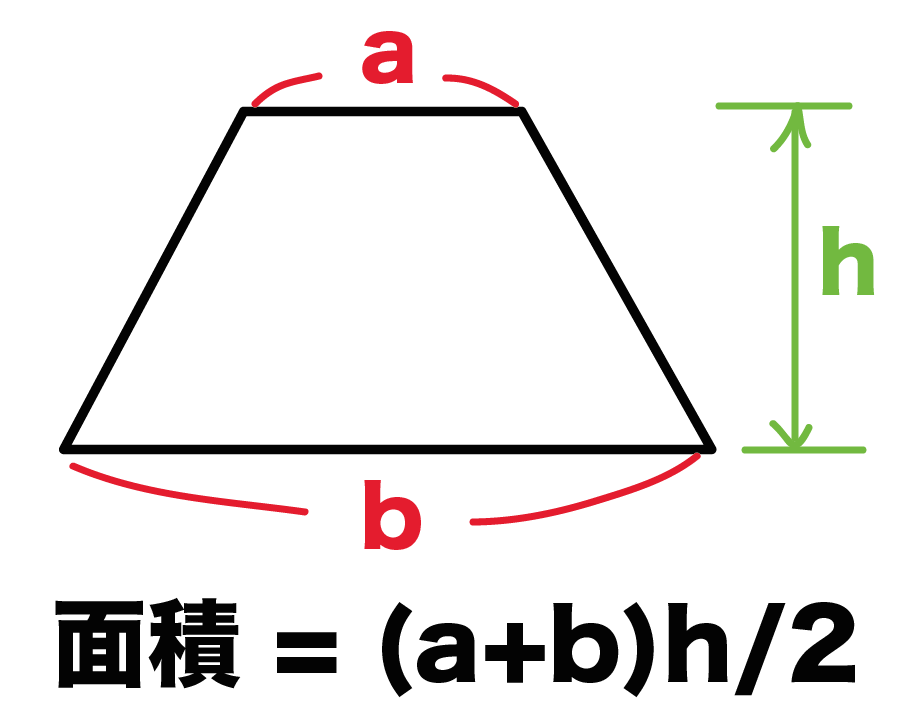
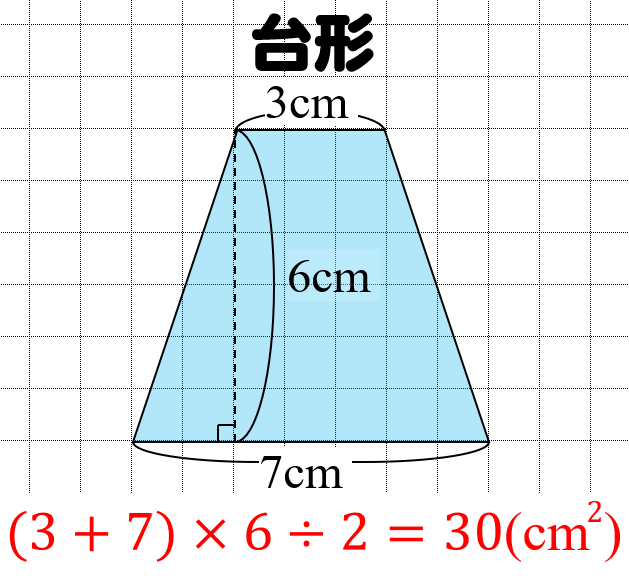
台形の面積の計算方法です。台形は、四角形のうち、一対の辺が平行になっているものです。平行になっている辺を上下に置くと、台のようになりますね。台形は、ラテン語でトラペジウムと呼びます。 面積の計算方法は (上底 下底) x 高さ ÷台形の面積を求める公式は、s = {(上底)(下底)}×(高さ)÷2 で表されます。このページでは、台形の面積の求め方を、計算問題と共に説明しています。また、公式の導き方も説明しています。台形の面積の公式 台形の面積は 『(上底下底)×高さ÷2 ÷ 2 』 で求めることができます。 たとえば以下のような問題の場合。 例題 上底3cm、下底7cm、高さ6cmの台形の面積を求めよ。 答えはこのように求めることができます。 (3 7)× 6÷2=30(cm2) ( 3 7) ×




小5算数 公式を考える 台形 Youtube



台形の面積公式 暗記よりも理解が大事 応用が利く図形問題の考え方 中学受験ナビ
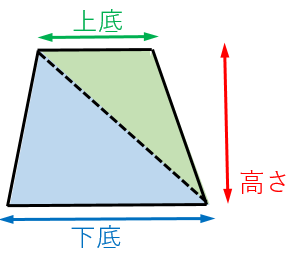
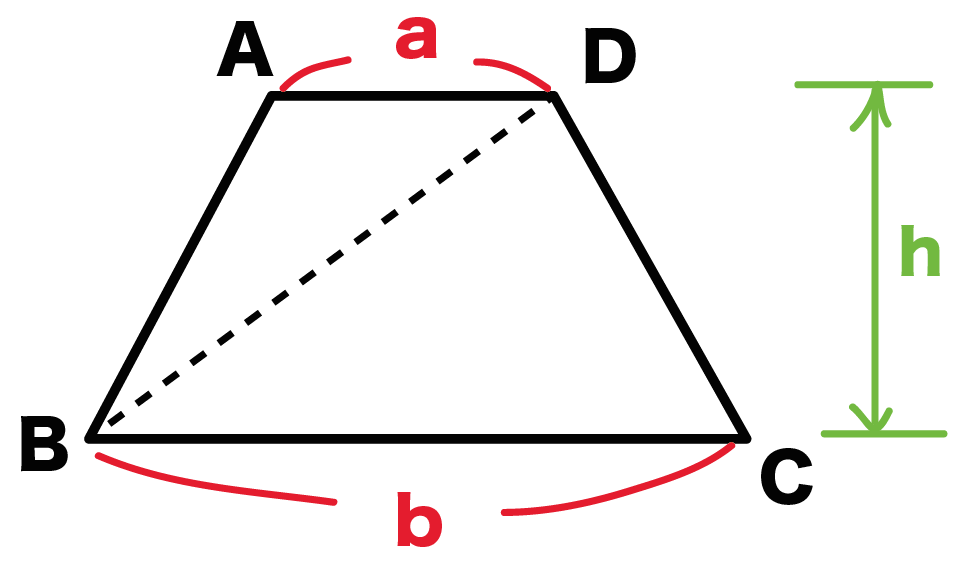
台形の面積はこれら2つを足し合わせることで、 (上底+下底)× 高さ ÷ 2 となります。 関連:図形の面積を求める公式たち19個 公式を忘れてしまっても大丈夫 台形の面積公式は、三角形の面積公式(底辺 × 高さ ÷ 2)がもとになっています。 もし台形の面積公式を忘れてしまっても、 対角台形の面積の公式を作る時に t偶然政野君と濱野君が考えた変形が t 台形の面積の ~式をよむと見えてきました ~ だったら (上底+下底)÷2を よこ と見て t高さを たて と見ると t よこ が(上底+下底)の半 分になって t たて が高さと同じになる 長方形にも変形できるよ u と声が 上がりまし本時では、台形の面積公式を扱う。一般的な指導では、既習 の図形に着目し多様な方法で面積を求めた後、例えば、右の図 2のような公式化を図りやすい方法を基にして、台形の面積公 式をつくることが多い。この倍積変形の方法は、三角形の面積



File 台形の面積1 Png Wikimedia Commons



台形の面積を求める公式 具体例で学ぶ数学
上底2cm、下底14cm、高さ6cmの台形になるので、面積は、 (2+14)×6÷2=48㎠ よって、 答え48㎠ まとめ いかがだったでしょうか?面積の応用問題は、補助線を入れてどんな図形の組み合わせでできているのか考えて公式を使うことが大切だとわかってもらえたと思います。 面積の問題は無数にある 例題4:台形の面積 ad // bc である台形 abcd において cd = 5, ac = 7, bc = 8, ∠adc = 1º とする。 このとき、台形 abcd の面積 s を求めよ。 だんだん難しくなってきましたね。 台形の面積公式や三角比の余弦定理をフル活用していきます。 解答 点 d から線分 bc に垂線 dh を下ろす。 ad // bc より ∠bcd台形の面積を求める公式は 台形の面積 上底 下底 高さ 台 形 の 面 積 = ( 上 底 下 底) × 高 さ ÷ 2 なので、 台形の面積 台 形 の 面 積 = ( 5 7) × 4 ÷ 2 = 12 × 4 ÷ 2 = 24 ( c m 2) になります。 次は小数点を含む台形の面積を計算します。
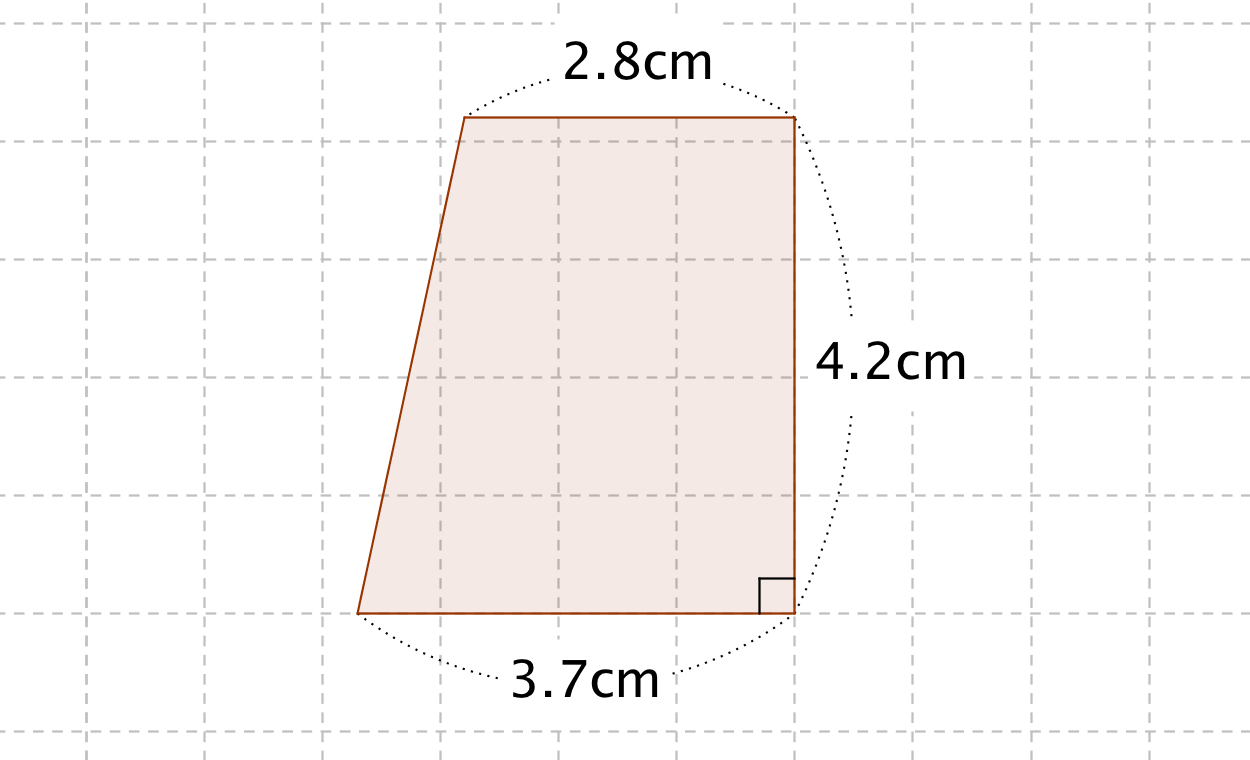



台形の面積の公式 算数の公式
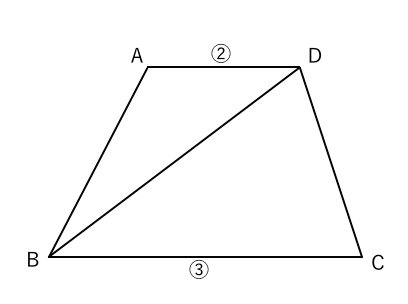



簡単に面積が何倍か求められる 使える編 苦手な数学を簡単に
台形公式で数値積分 樋口さぶろお dx = (y = 0, y = f(x), x = a,x = b に囲まれた部分の面積) 原始関数F (F0 = f)を利用したF(x)b a というのは, ラッキーなら 使えることもある計算テクニックにすぎない F(x) を求めることができないこともある 例e¡x2 ¤ § ¥ 栗原x51 ƒ 樋口さぶろお(数理情報学科) 台形Trapz は、台形法を使って数値を積分します。このメソッドでは、領域を台形に分割してより簡単に計算できるようにすることで、間隔の積分を近似します。たとえば、以下は 8 つの等間隔な台形を使用した正弦関数の台形積分です。 N1 の等間隔の点での積分では、近似は次のようになります台形abedの面積は(12+6)×27÷2=243cm 2 。 三角形dfeと三角形abfは相似なので、 三角形dfeと三角形afdと三角形fbeと 三角形abfの面積の比は1:2:2:4。 台形abedの面積を9とすると、黄緑の部分の面積は4。




台的体积怎么求 台形体积计算方法 三人行教育网 Www 3rxing Org
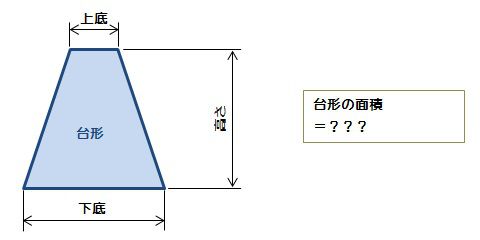



台形の面積 算数の公式覚えてますか
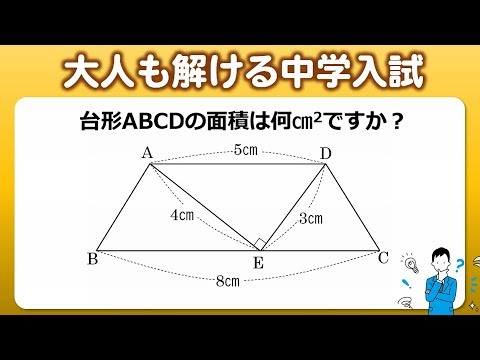



大人も解ける中学入試 標準レベルの面積問題 Youtube



台形の面積の計算 自動計算サイト




台形の面積の公式 算数の公式



なぜ 台形の面積は 上底 下底 高さ 2 なのか を説明します おかわりドリル




高さがわからない台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



数学 台形を4分割した図形パターン 面積比 集中特訓 3 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典




台形の面積の求め方 公式が誰でも一目でわかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ



小学5年生 算数 無料問題集 台形の面積 おかわりドリル
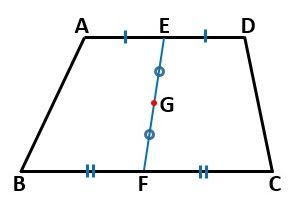



台形の面積の2等分線 東久留米 学習塾 塾長ブログ




台形の面積の求めかたは 忘れても大丈夫 公式は自分でつくろう
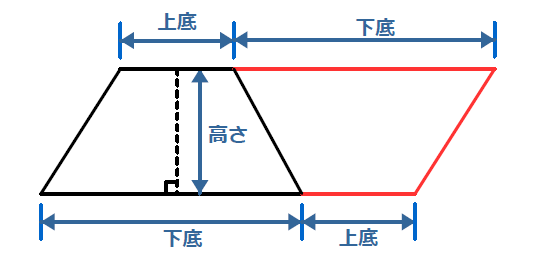



台形の面積計算 ゆるゆるプログラミング




台形面積 はかせどん わさっきhb
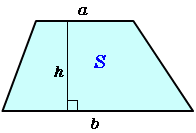



台形の面積 高精度計算サイト
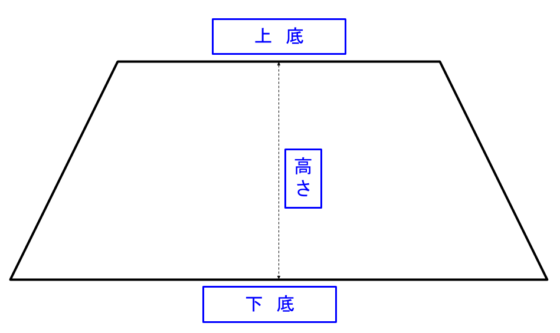



台形の面積 計算機 基本公式と高さが分からないときの求め方 やまでら くみこ のレシピ




台形の面積 における導入問題の工夫 三角形と台形の面積 どちらが大きい 私の実践 私の工夫アーカイブ一覧 授業支援 サポート資料 算数 小学校 知が啓く 教科書の啓林館




小学5年生 ひし形 台形の面積 算数 Active Learning 学院



台形の面積 算数の公式覚えてますか
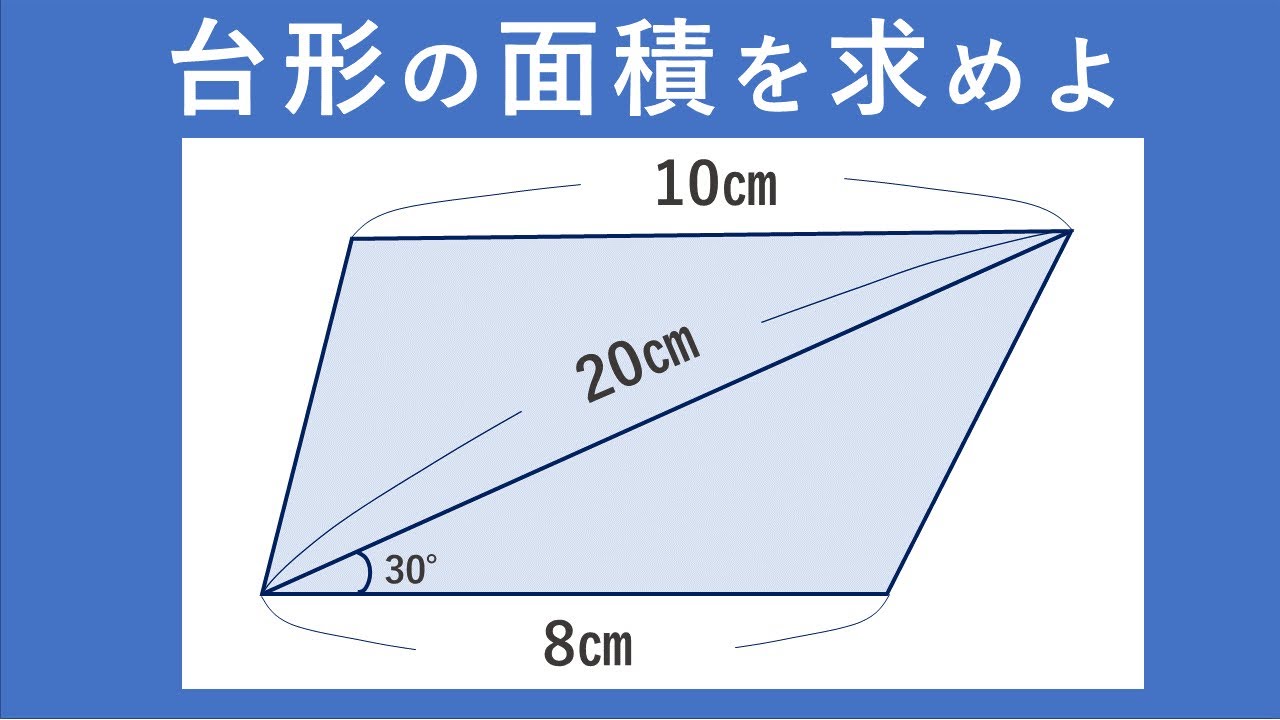



シンプルで難しい問題 台形の面積を求めよ Youtube




台形の面積を2等分する方法を教えてください Clear




台形の面積を求める公式 具体例で学ぶ数学




台形の面積の求め方 公式と計算例




台形の面積の求めかたは 忘れても大丈夫 公式は自分でつくろう



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典




なぜ 台形の面積は 上底 下底 高さ 2 なのか を説明します おかわりドリル



第5学年 面積 台形 私の実践 私の工夫アーカイブ一覧 授業支援 サポート資料 算数 小学校 知が啓く 教科書の啓林館



台形の面積計算 ゆるゆるプログラミング



なぜ 台形の面積は 上底 下底 高さ 2 なのか を説明します おかわりドリル




台形の面積の求め方 公式と計算例



数学 台形を4分割した図形パターン 面積比 集中特訓 3 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典



三角形と台形の面積




台形の面積の求め方 公式と計算例



台形の公式は必要か



台形の面積は公式が分からなくても大丈夫 対角線を引いたり等積変形を利用したりする求め方とは みけねこ小学校




File 台形の面積2 Png Wikimedia Commons




相似13 高さが等しい台形の面積比 Youtube



簡単公式 台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




小学5年生 算数 11月 台形の面積 いろいろな図形の面積 割合 百分率の意味と求め方 練習問題プリント 栄光ゼミナール ちびむすドリル 小学生学習教材 スペシャルコラボ




相似 台形と面積比の問題を徹底解説 数スタ



台形の面積の公式 小学生に教えるための分かりやすい解説 数学fun




台形の面積の公式 小学生に教えるための分かりやすい解説 数学fun



簡単公式 台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




台形の面積は公式が分からなくても大丈夫 対角線を引いたり等積変形を利用したりする求め方とは みけねこ小学校




よく出る台形の面積比 算数 過去問で基本を鍛える 12 勉強法のバイブル 帝都大学へのビジョン




四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ



3分で分かる 台形の面積の求め方 公式についてわかりやすく 合格サプリ




小5 面積 台形の面積の求め方 日本語版 Youtube




台形 の面積 計算ドリル 問題集 数学fun



3分で分かる 台形の面積の求め方 公式についてわかりやすく 合格サプリ




台形の面積の求め方 公式 小学生 中学生の勉強
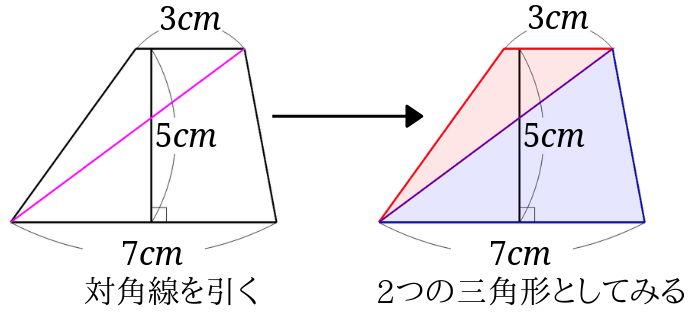



台形の面積は公式が分からなくても大丈夫 対角線を引いたり等積変形を利用したりする求め方とは みけねこ小学校




台形の面積の公式 小学生に教えるための分かりやすい解説 数学fun




台形の面積の求めかたは 忘れても大丈夫 公式は自分でつくろう



台形の面積公式 算数と図形 理数系無料オンライン学習 Kori
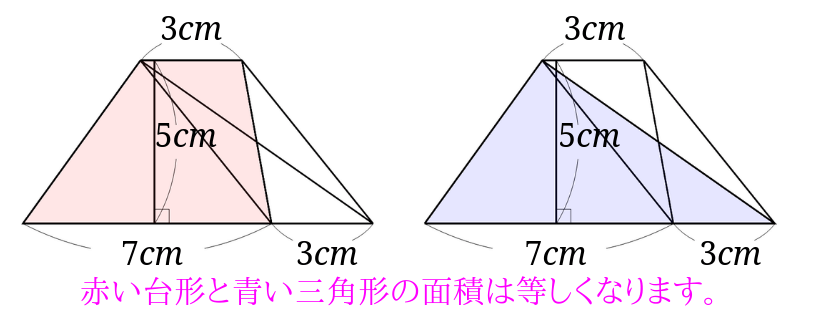



台形の面積は公式が分からなくても大丈夫 対角線を引いたり等積変形を利用したりする求め方とは みけねこ小学校
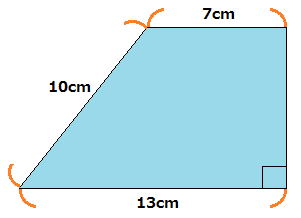



台形の面積の解答と解説 多目的ルーム 楽天ブログ




台形の面積の求め方 公式 小学生 中学生の勉強




台形の面積の求め方 公式と計算例




簡単公式 台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
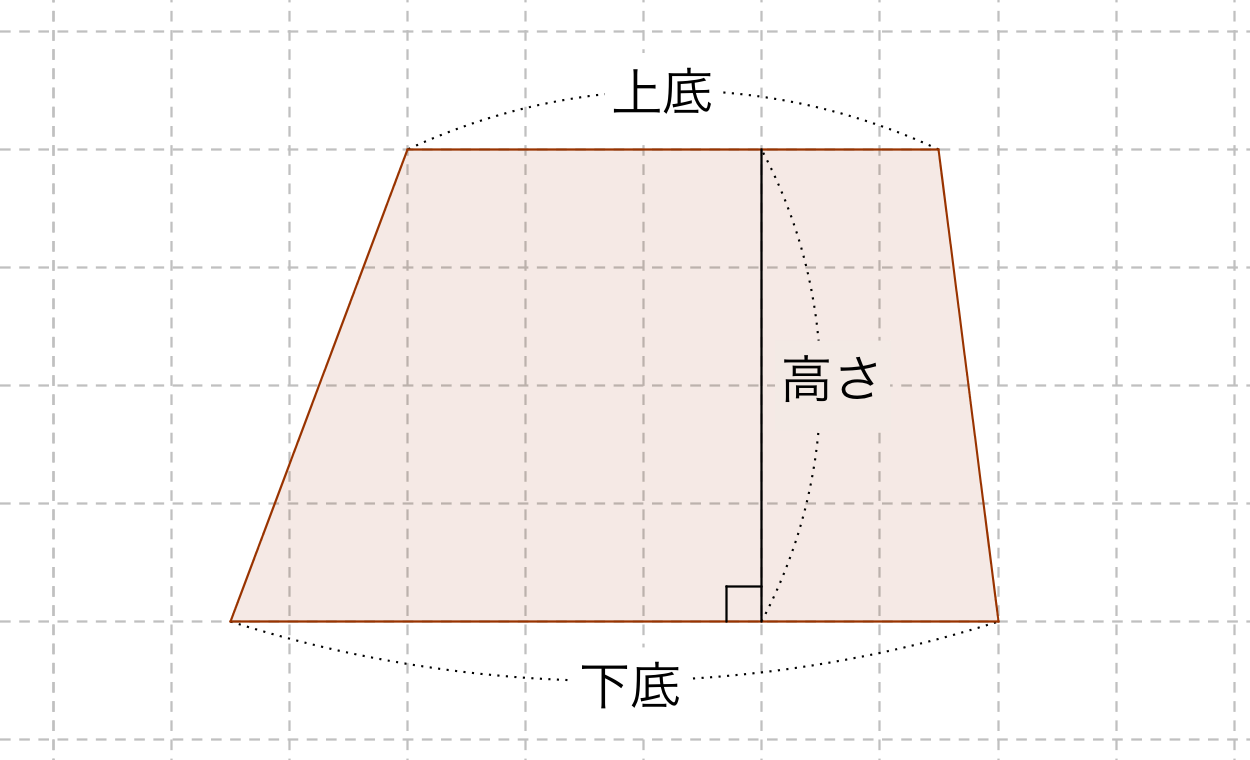



台形の面積の公式 算数の公式




3分で分かる 台形の面積の求め方 公式についてわかりやすく 合格サプリ



3分で分かる 台形の面積の求め方 公式についてわかりやすく 合格サプリ
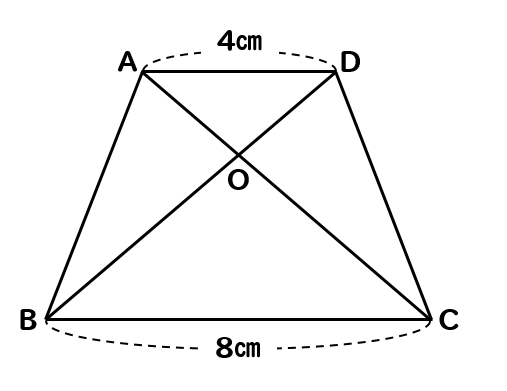



相似 台形と面積比の問題を徹底解説 数スタ
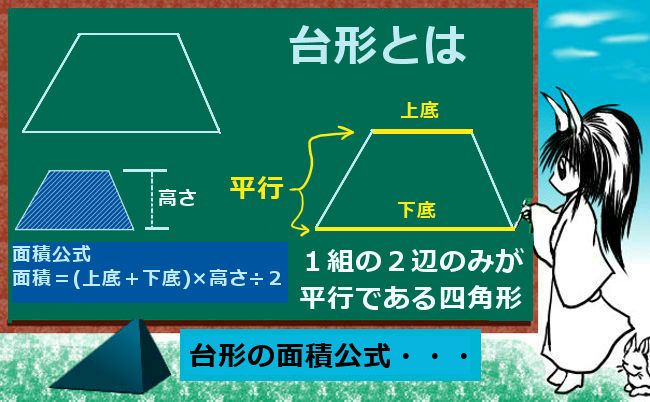



台形の面積公式 算数と図形 理数系無料オンライン学習 Kori




面積 台形 ひし形の面積 01 台形の面積 Youtube



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典




Amazon Com Area 面積計算 Apps Games
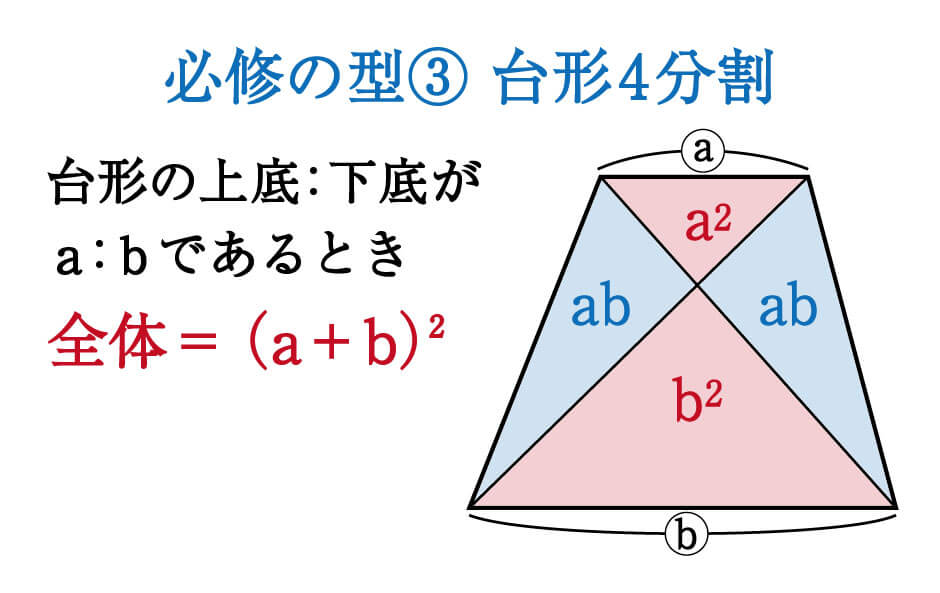



数学 台形を4分割した図形パターン 面積比 集中特訓 3 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




台形の面積の求め方 公式が誰でも一目でわかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ




高さがわからない台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




台形の面積の公式 ゆとり教育で求め方がわからない人は見て 中学や高校の数学の計算問題




台形の面積の求めかたは 忘れても大丈夫 公式は自分でつくろう



台形の面積 算数の公式覚えてますか
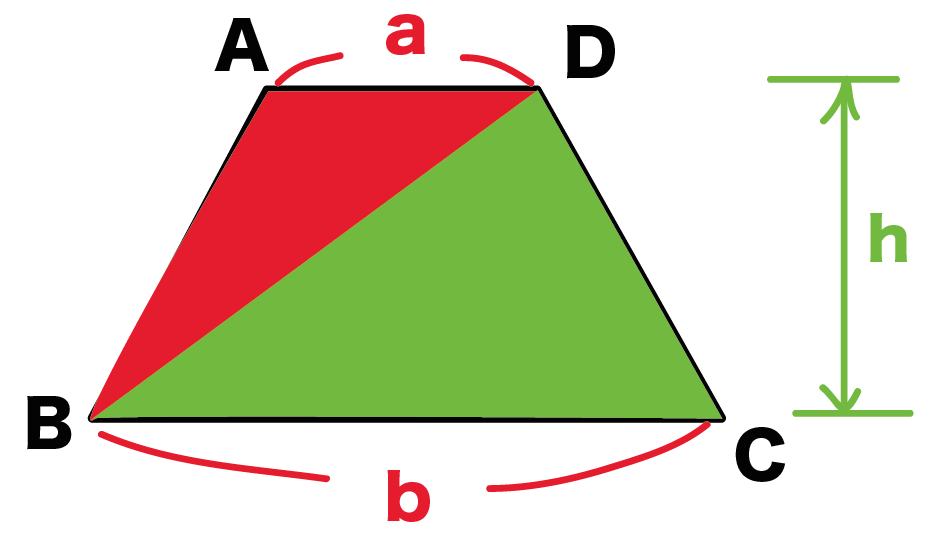



簡単公式 台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




台形の面積の求め方 公式と計算例




図形の問題 台形の面積 いつもいろいろな方から丁寧な解答をいだただ 数学 教えて Goo




5年算数 台形の面積 指導実践 ネコ好きな学校の先生の日常
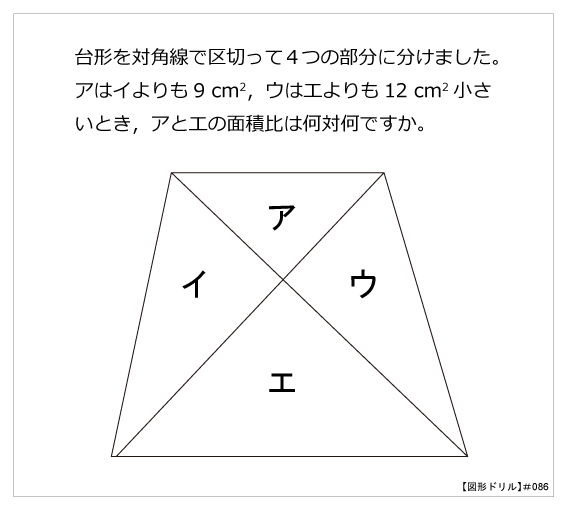



図形ドリル 第86問 台形の面積比 算数星人のweb問題集 中学受験算数の問題に挑戦
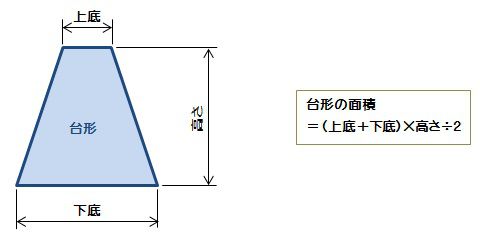



台形の面積 算数の公式覚えてますか



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典
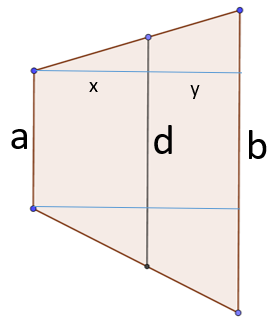



台形の面積を2等分する線分の長さ メソポタミア文明の人は知ってたらしいで キソカラ



台形内の三角形の面積 女子学院中学 2012年 どう解く 中学受験算数
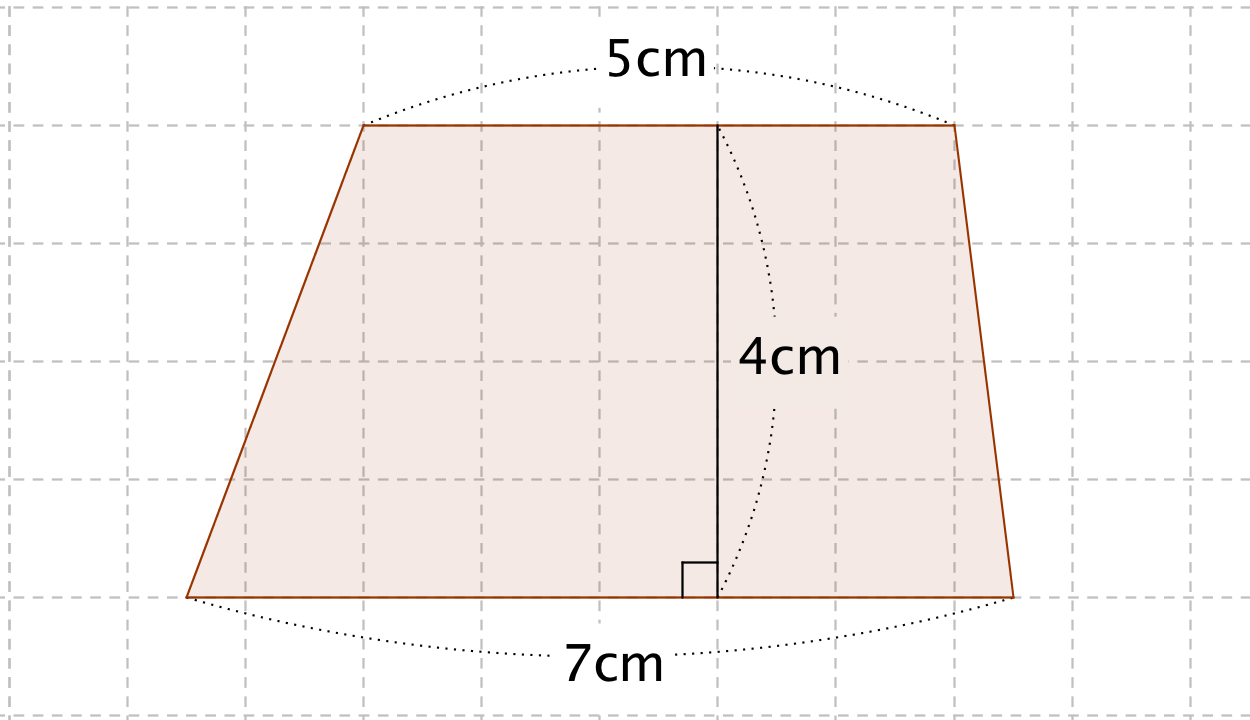



台形の面積の公式 算数の公式



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典




台形の面積の求めかたは 忘れても大丈夫 公式は自分でつくろう




小5 台形 面積の求め方 日本語版 Youtube




台形の面積を二等分する直線 Youtube



0 件のコメント:
コメントを投稿